题目内容
已知函数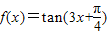 .
.(1)求
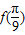 的值;
的值;(2)设
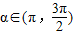 ,若
,若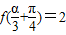 ,求
,求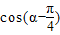 的值.
的值.
【答案】分析:(1)直接利用两角和的正切公式求出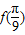 的值.
的值.
(2)由条件利用诱导公式求出tanα=2,再利用同角三角函数的基本关系求出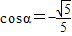 ,
,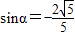 .再利用两角和的余弦公式求出
.再利用两角和的余弦公式求出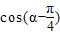 的值.
的值.
解答:解:(1)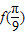 =
=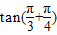 …(1分)=
…(1分)=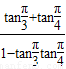 …(3分)=
…(3分)=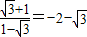 .…(4分)
.…(4分)
(2)因为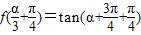 …(5分)=tan(α+π)…(6分)=tanα=2.…(7分)
…(5分)=tan(α+π)…(6分)=tanα=2.…(7分)
所以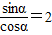 ,即sinα=2cosα. ①
,即sinα=2cosα. ①
因为sin2α+cos2α=1,②
由①、②解得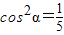 .…(9分)
.…(9分)
因为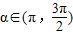 ,所以
,所以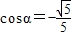 ,
,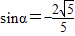 .…(10分)
.…(10分)
所以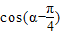 =
=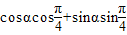 …(11分)=
…(11分)=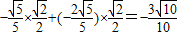 .…(12分)
.…(12分)
点评:本小题主要考查两角和的正切、诱导公式、同角三角函数的基本关系和两角差的余弦等知识,考查化归与转化的数学思想方法,以及运算求解能力,属于中档题.
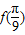 的值.
的值.(2)由条件利用诱导公式求出tanα=2,再利用同角三角函数的基本关系求出
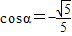 ,
,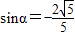 .再利用两角和的余弦公式求出
.再利用两角和的余弦公式求出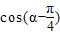 的值.
的值.解答:解:(1)
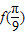 =
=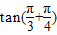 …(1分)=
…(1分)=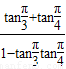 …(3分)=
…(3分)=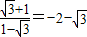 .…(4分)
.…(4分)(2)因为
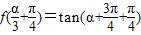 …(5分)=tan(α+π)…(6分)=tanα=2.…(7分)
…(5分)=tan(α+π)…(6分)=tanα=2.…(7分)所以
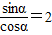 ,即sinα=2cosα. ①
,即sinα=2cosα. ①因为sin2α+cos2α=1,②
由①、②解得
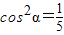 .…(9分)
.…(9分)因为
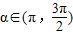 ,所以
,所以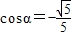 ,
,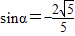 .…(10分)
.…(10分)所以
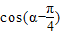 =
=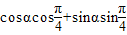 …(11分)=
…(11分)=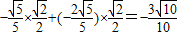 .…(12分)
.…(12分)点评:本小题主要考查两角和的正切、诱导公式、同角三角函数的基本关系和两角差的余弦等知识,考查化归与转化的数学思想方法,以及运算求解能力,属于中档题.

练习册系列答案
相关题目
 .
. 的值;
的值;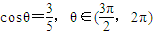 ,求
,求 .
. .
. 的值;
的值; .
. 的单调区间;
的单调区间; ,若对任意
,若对任意 ,总存在
,总存在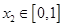 ,使得
,使得 ,求实数
,求实数 的取值范围.
的取值范围.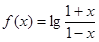 ,(1)求
,(1)求 的定义域;
(2)使
的定义域;
(2)使 的
的 的取值范围.
的取值范围. ,(1)求
,(1)求 的最小正周期;(2)求
的最小正周期;(2)求 的集合。
的集合。