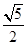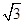题目内容
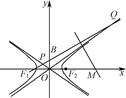
如图,F1、F2分别是双曲线C: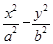 =1(a,b>0)的左、右焦点,B是虚轴的端点,直线F1B与C的两条渐近线分别交于P、Q两点,线段PQ的垂直平分线与x轴交于点M.若MF2=F1F2,则C的离心率是________.
=1(a,b>0)的左、右焦点,B是虚轴的端点,直线F1B与C的两条渐近线分别交于P、Q两点,线段PQ的垂直平分线与x轴交于点M.若MF2=F1F2,则C的离心率是________.
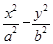 =1(a,b>0)的左、右焦点,B是虚轴的端点,直线F1B与C的两条渐近线分别交于P、Q两点,线段PQ的垂直平分线与x轴交于点M.若MF2=F1F2,则C的离心率是________.
=1(a,b>0)的左、右焦点,B是虚轴的端点,直线F1B与C的两条渐近线分别交于P、Q两点,线段PQ的垂直平分线与x轴交于点M.若MF2=F1F2,则C的离心率是________.
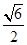
设双曲线的焦点坐标为F1(-c,0),F2(c,0).
∵B(0,b),∴F1B所在的直线为-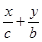 =1.①
=1.①
双曲线渐近线为y=± x,由
x,由 得Q
得Q .
.
由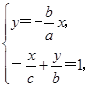 得P
得P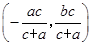 ,∴PQ的中点坐标为
,∴PQ的中点坐标为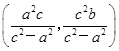 .
.
由a2+b2=c2得,PQ的中点坐标可化为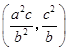 .
.
直线F1B的斜率为k=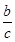 ,∴PQ的垂直平分线为y-
,∴PQ的垂直平分线为y- =-
=-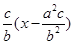 .
.
令y=0,得x= +c,∴M
+c,∴M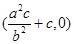 ,∴F2M=
,∴F2M= .
.
由MF2=F1F2得 =
=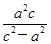 =2c,即3a2=2c2,∴e2=
=2c,即3a2=2c2,∴e2=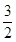 ,∴e=
,∴e=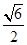
∵B(0,b),∴F1B所在的直线为-
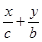 =1.①
=1.①双曲线渐近线为y=±
 x,由
x,由 得Q
得Q .
.由
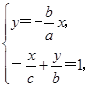 得P
得P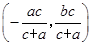 ,∴PQ的中点坐标为
,∴PQ的中点坐标为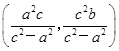 .
.由a2+b2=c2得,PQ的中点坐标可化为
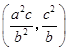 .
.直线F1B的斜率为k=
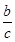 ,∴PQ的垂直平分线为y-
,∴PQ的垂直平分线为y- =-
=-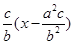 .
.令y=0,得x=
 +c,∴M
+c,∴M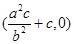 ,∴F2M=
,∴F2M= .
.由MF2=F1F2得
 =
=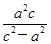 =2c,即3a2=2c2,∴e2=
=2c,即3a2=2c2,∴e2=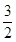 ,∴e=
,∴e=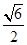

练习册系列答案
相关题目
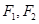 是双曲线
是双曲线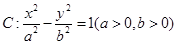 的两个焦点,
的两个焦点, 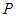 是
是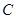 上一点,若
上一点,若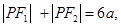 且
且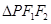 的最小内角为
的最小内角为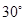 ,则
,则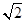
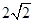
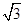
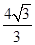
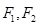 分别是双曲线
分别是双曲线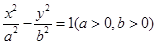 的左右焦点,过点
的左右焦点,过点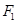 的直线
的直线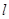 与双曲线的左右两支分别交于
与双曲线的左右两支分别交于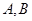 两点。若
两点。若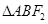 是等边三角形,则该双曲线的离心率为( )
是等边三角形,则该双曲线的离心率为( ) 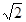
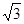
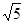
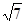
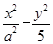 =1的右焦点为(3,0),则该双曲线的离心率为________.
=1的右焦点为(3,0),则该双曲线的离心率为________.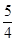 ,则双曲线的标准方程为______________________.
,则双曲线的标准方程为______________________.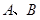 为两个定点,
为两个定点,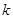 为非零常数,
为非零常数, ,则动点
,则动点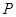 的轨迹为双曲线;②过定圆
的轨迹为双曲线;②过定圆 上一定点
上一定点 作圆的动点弦
作圆的动点弦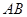 ,
, 为坐标原点,若
为坐标原点,若 则动点
则动点 是
是 的一内角,且
的一内角,且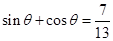 ,则
,则 表示焦点在
表示焦点在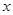 轴上的双曲线;④已知两定点
轴上的双曲线;④已知两定点 和一动点
和一动点 ,则点
,则点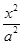 -
-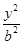 =1(a>0,b>0)的离心率为2,一个焦点与抛物线y2=16x的焦点相同,则双曲线的渐近线方程为( )
=1(a>0,b>0)的离心率为2,一个焦点与抛物线y2=16x的焦点相同,则双曲线的渐近线方程为( )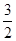 x
x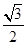 x
x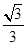 x
x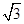 x
x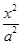 -
-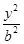 =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为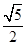 ,则C的渐近线方程为( )
,则C的渐近线方程为( ) x
x x
x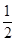 x
x
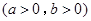 的渐近线方程是
的渐近线方程是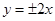 ,则其离心率为( )
,则其离心率为( )