题目内容
（本小题满分12分）
已知
，记点P的轨迹为E，直线
过点
且与轨迹E交于
两点。
（1）无论直线绕点怎样转动，在x轴上总存在定点
，使
恒成立，求实数m的值。
（2）过做直线
的垂线
，垂足分别为A、B，记
=
，球的取值范围。
（本小题满分12分）
解：（1）由
知，点P的轨迹E是以F1、F2为焦点的双曲线的右支，由
，故轨迹E的方程为
当直线l的斜率存在时，设直线方程为
，与双曲线方程联立消y得
，
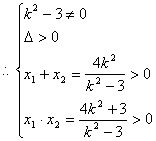
解得k2 >3
，
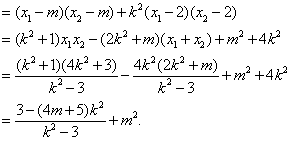
故得
对任意的
恒成立，
∴当m =－1时，MP⊥MQ. ………………………………………………6分
当直线l的斜率不存在时，由
知结论也成立，
综上，当m =－1时，MP⊥MQ. ………………………………………………7分
（2）
是双曲线的右准线，
由双曲线定义得：
，………………8分
方法一：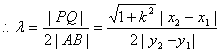
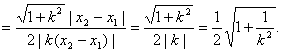
，……………10分
注意到直线的斜率不存在时，
，……11分
综上，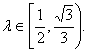
………………………………………………12分
方法二：设直线PQ的倾斜角为θ，由于直线PQ与双曲线右支有二个交点，
，过Q作QC⊥PA，垂足为C，则
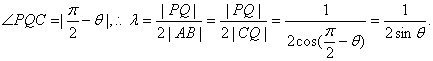……11分
由
故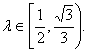： ………………12分
练习册系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
