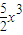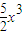题目内容
在二项式（1-x）11展开式中含x奇次幂的项的系数和等于
- A.210
- B.-210
- C.-211
- D.-25
B
分析：设出展开式，分别令x为1，-1得到两等式，两式相减得到展开式中含x奇次幂的项的系数和．
解答：令（1-x）11=a0+a1x+a2x2+…+a11x11
令x=1得0=a0+a1+a2+…+a11
令x=-1得211=a0-a1+a2-a3…+a10-a11
两式相减得-211=2（a1+a3+…+a11）
解得-210=（a1+a3+…+a11）
故选B
点评：本题考查求展开式的系数和常用的方法是赋值法．
分析：设出展开式，分别令x为1，-1得到两等式，两式相减得到展开式中含x奇次幂的项的系数和．
解答：令（1-x）11=a0+a1x+a2x2+…+a11x11
令x=1得0=a0+a1+a2+…+a11
令x=-1得211=a0-a1+a2-a3…+a10-a11
两式相减得-211=2（a1+a3+…+a11）
解得-210=（a1+a3+…+a11）
故选B
点评：本题考查求展开式的系数和常用的方法是赋值法．
练习册系列答案
相关题目
x）n的展开式中，偶数项二项式系数为32，则展开式的中间项为（ ）．
