题目内容
已知数列{an}的前n项和为Sn,且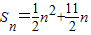 (n∈N*).
(n∈N*).(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设
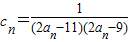 ,数列{cn}的前n项和为Tn,求使不等式Tn
,数列{cn}的前n项和为Tn,求使不等式Tn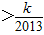 对一切n∈N*都成立的最大正整数k的值;
对一切n∈N*都成立的最大正整数k的值;(Ⅲ)设f(n)=
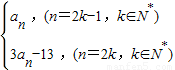 是否存在m∈N*,使得f(m+15)=5f(m)成立?若存在,求出m的值;若不存在,请说明理由.
是否存在m∈N*,使得f(m+15)=5f(m)成立?若存在,求出m的值;若不存在,请说明理由.
【答案】分析:(I)利用当n=1时,a1=S1,当n≥2时,an=Sn-Sn-1即可得出;
(II)利用“裂项求和”即可得出Tn,再利用其单调性即可得出k的最大值;
(III)利用(I)求出f(n),再对m分为奇数和偶数讨论即可得出.
解答:解:(I)当n=1时,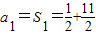 =6.
=6.
当n≥2时,an=Sn-Sn-1=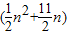 -
-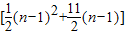 =n+5.
=n+5.
此式对于n=1时也成立.
因此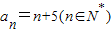 .
.
(II)∵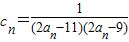 =
=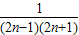 =
=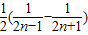 ,
,
∴Tn=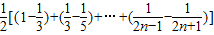 =
=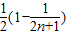 =
=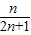 .
.
∵Tn+1-Tn=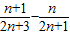 =
=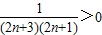 ,∴数列{
,∴数列{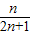 }单调递增,
}单调递增,
∴(Tn)min=T1= .令
.令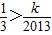 ,解得k<671,∴kmax=670.
,解得k<671,∴kmax=670.
(III)f(n)=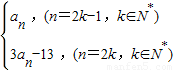 =
=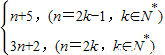 ,
,
(1)当m为奇数时,m+15为偶数,∴3m+47=5m+25,解得m=11.
(2)当m为偶数时,m+15为奇数,∴m+20=15m+10,解得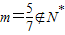 (舍去).
(舍去).
综上可知:存在唯一的正整数m=11,使得f(m+15)=5f(m)成立.
点评:熟练掌握“利用当n=1时,a1=S1,当n≥2时,an=Sn-Sn-1即可得出an”、“裂项求和”、数列的单调性、分类讨论的思想方法等是解题的关键.
(II)利用“裂项求和”即可得出Tn,再利用其单调性即可得出k的最大值;
(III)利用(I)求出f(n),再对m分为奇数和偶数讨论即可得出.
解答:解:(I)当n=1时,
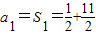 =6.
=6.当n≥2时,an=Sn-Sn-1=
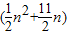 -
-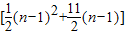 =n+5.
=n+5.此式对于n=1时也成立.
因此
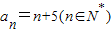 .
.(II)∵
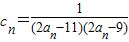 =
=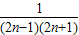 =
=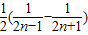 ,
,∴Tn=
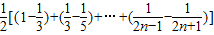 =
=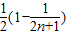 =
=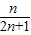 .
.∵Tn+1-Tn=
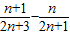 =
=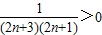 ,∴数列{
,∴数列{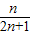 }单调递增,
}单调递增,∴(Tn)min=T1=
 .令
.令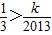 ,解得k<671,∴kmax=670.
,解得k<671,∴kmax=670.(III)f(n)=
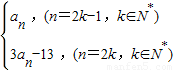 =
=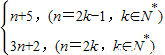 ,
,(1)当m为奇数时,m+15为偶数,∴3m+47=5m+25,解得m=11.
(2)当m为偶数时,m+15为奇数,∴m+20=15m+10,解得
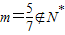 (舍去).
(舍去).综上可知:存在唯一的正整数m=11,使得f(m+15)=5f(m)成立.
点评:熟练掌握“利用当n=1时,a1=S1,当n≥2时,an=Sn-Sn-1即可得出an”、“裂项求和”、数列的单调性、分类讨论的思想方法等是解题的关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |