题目内容
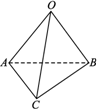
如下图,在△OAB中,|OA|=|OB|=4,点P分线段AB所成的比为3:1,以OA、OB所在直线为渐近线的双曲线M恰好经过点P,且离心率为2.(1)求双曲线M的标准方程;
(2)若直线y=kx+m(k≠0,m≠0)与双曲线M交于不同的两点E、F,且E、F两点都在以Q(0,-3)为圆心的同一圆上,求实数m的取值范围.

【答案】分析:(1)根据曲线M的离心率为2,可设双曲线M的方程为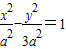 ,从而可得∠BOx=60°,可求得B(2,2
,从而可得∠BOx=60°,可求得B(2,2 ),A(2,
),A(2,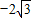 ),根据点P分线段AB所成的比为3:1得P(2,
),根据点P分线段AB所成的比为3:1得P(2,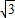 ),代入双曲线方程,即可求出双曲线M的方程;
),代入双曲线方程,即可求出双曲线M的方程;
(2)将执行方程与双曲线方程联立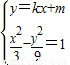 ,消去y得(k2-3)x2+2kmx+m2+9=0
,消去y得(k2-3)x2+2kmx+m2+9=0
根据直线y=kx+m(k≠0,m≠0)与双曲线M交于不同的两点,可得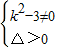 ,从而有
,从而有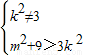
利用E、F两点都在以Q(0,-3)为圆心的同一圆上,所以NQ⊥EF,从而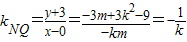
由此得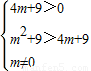 ,从而求出实数m的取值范围.
,从而求出实数m的取值范围.
解答:解:(1)因为曲线M的离心率为2,所以可设双曲线M的方程为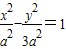
由此可得渐近线的斜率k=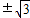
∴∠BOx=60°,
从而B(2,2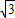 ),A(2,
),A(2,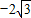 )
)
又因为点P分线段AB所成的比为3:1
故P(2,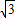 ),代入双曲线方程得a2=3,
),代入双曲线方程得a2=3,
故双曲线M的方程为: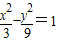
(2)如图所示,由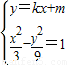 ⇒(k2-3)x2+2kmx+m2+9=0
⇒(k2-3)x2+2kmx+m2+9=0
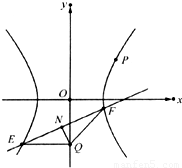 设E(x1,y1)、F(x2,y2),线段EF的中点为N(x,y),则有
设E(x1,y1)、F(x2,y2),线段EF的中点为N(x,y),则有
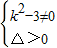 ⇒
⇒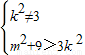 ①
①
由韦达定理得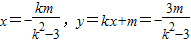
因为E、F两点都在以Q(0,-3)为圆心的同一圆上,所以NQ⊥EF,
即
∴3k2=4m+9 ②
由①②得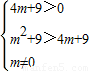
∴m>4或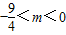
点评:本题以双曲线的几何性质为载体,考查双曲线的标准方程,考查直线与双曲线的位置关系,考查学生分析解决问题的能力,综合性强,有难度.
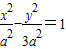 ,从而可得∠BOx=60°,可求得B(2,2
,从而可得∠BOx=60°,可求得B(2,2 ),A(2,
),A(2,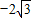 ),根据点P分线段AB所成的比为3:1得P(2,
),根据点P分线段AB所成的比为3:1得P(2,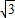 ),代入双曲线方程,即可求出双曲线M的方程;
),代入双曲线方程,即可求出双曲线M的方程;(2)将执行方程与双曲线方程联立
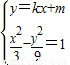 ,消去y得(k2-3)x2+2kmx+m2+9=0
,消去y得(k2-3)x2+2kmx+m2+9=0根据直线y=kx+m(k≠0,m≠0)与双曲线M交于不同的两点,可得
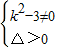 ,从而有
,从而有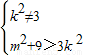
利用E、F两点都在以Q(0,-3)为圆心的同一圆上,所以NQ⊥EF,从而
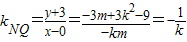
由此得
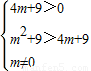 ,从而求出实数m的取值范围.
,从而求出实数m的取值范围.解答:解:(1)因为曲线M的离心率为2,所以可设双曲线M的方程为
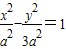
由此可得渐近线的斜率k=
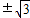
∴∠BOx=60°,
从而B(2,2
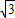 ),A(2,
),A(2,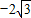 )
)又因为点P分线段AB所成的比为3:1
故P(2,
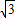 ),代入双曲线方程得a2=3,
),代入双曲线方程得a2=3,故双曲线M的方程为:
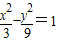
(2)如图所示,由
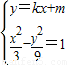 ⇒(k2-3)x2+2kmx+m2+9=0
⇒(k2-3)x2+2kmx+m2+9=0 设E(x1,y1)、F(x2,y2),线段EF的中点为N(x,y),则有
设E(x1,y1)、F(x2,y2),线段EF的中点为N(x,y),则有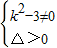 ⇒
⇒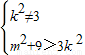 ①
①由韦达定理得
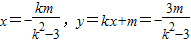
因为E、F两点都在以Q(0,-3)为圆心的同一圆上,所以NQ⊥EF,
即

∴3k2=4m+9 ②
由①②得
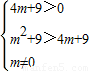
∴m>4或
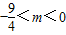
点评:本题以双曲线的几何性质为载体,考查双曲线的标准方程,考查直线与双曲线的位置关系,考查学生分析解决问题的能力,综合性强,有难度.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
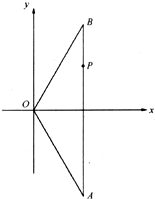 (2006•广州一模)如下图,在△OAB中,|OA|=|OB|=4,点P分线段AB所成的比为3:1,以OA、OB所在直线为渐近线的双曲线M恰好经过点P,且离心率为2.
(2006•广州一模)如下图,在△OAB中,|OA|=|OB|=4,点P分线段AB所成的比为3:1,以OA、OB所在直线为渐近线的双曲线M恰好经过点P,且离心率为2.