题目内容
 (2012•广东模拟)如图,P是抛物线C:y=
(2012•广东模拟)如图,P是抛物线C:y=| 1 |
| 2 |
(1)当点P的横坐标为2时,求直线l的方程;
(2)若
| OP |
| OQ |
分析:(Ⅰ)先求点P的坐标,利用导数求过点P的切线的斜率,从而可得直线l的斜率,即可求出直线l的方程;
(Ⅱ)设P(x0,y0),求出直线l的方程为 y-
=-
(x-x0),利用
•
=0,可得过点P,Q,O的圆的圆心为PQ的中点,将直线与抛物线联立,即可求出PQ的中点的坐标与圆的半径,从而可得过点P,Q,O的圆的方程.
(Ⅱ)设P(x0,y0),求出直线l的方程为 y-
| 1 |
| 2 |
| x | 2 0 |
| 1 |
| x0 |
| OP |
| OQ |
解答:解:(Ⅰ)把x=2代入y=
x2,得y=2,∴点P的坐标为(2,2).…(1分)
由 y=
x2,①得y'=x,
∴过点P的切线的斜率k切=2,…(2分)
直线l的斜率k1=-
=-
,…(3分)
∴直线l的方程为y-2=-
(x-2),即x+2y-6=0…(4分)
(Ⅱ)设P(x0,y0),则y0=
.
∵过点P的切线斜率k切=x0,因为x0≠0.
∴直线l的斜率k1=-
=-
,
直线l的方程为 y-
=-
(x-x0).②…(5分)
设Q(x1,y1),且M(x,y)为PQ的中点,
因为
•
=0,所以过点P,Q,O的圆的圆心为M(x,y),半径为r=|PM|,…(6分)
且x0x1+y0y1=x0x1+
x02x12=0,…(8分)
所以x0x1=0(舍去)或x0x1=-4…(9分)
联立①②消去y,得x2+
x-xo2-2=0
由题意知x0,x1为方程的两根,
所以x0x1=-x02-2=-4,又因为x0>0,所以x0=
,y0=1;
所以x1=-2
,y1=4…(11分)
∵M是PQ的中点,∴
…(12分)
∴r2=(x-x0)2+(y-y0)2=
…(13分)
所以过点P,Q,O的圆的方程为(x+
)2+(y-
)2=
…(14分)
| 1 |
| 2 |
由 y=
| 1 |
| 2 |
∴过点P的切线的斜率k切=2,…(2分)
直线l的斜率k1=-
| 1 |
| k切 |
| 1 |
| 2 |
∴直线l的方程为y-2=-
| 1 |
| 2 |
(Ⅱ)设P(x0,y0),则y0=
| 1 |
| 2 |
| x | 2 0 |
∵过点P的切线斜率k切=x0,因为x0≠0.
∴直线l的斜率k1=-
| 1 |
| k切 |
| 1 |
| x0 |
直线l的方程为 y-
| 1 |
| 2 |
| x | 2 0 |
| 1 |
| x0 |
设Q(x1,y1),且M(x,y)为PQ的中点,
因为
| OP |
| OQ |
且x0x1+y0y1=x0x1+
| 1 |
| 4 |
所以x0x1=0(舍去)或x0x1=-4…(9分)
联立①②消去y,得x2+
| 2 |
| x0 |
由题意知x0,x1为方程的两根,
所以x0x1=-x02-2=-4,又因为x0>0,所以x0=
| 2 |
所以x1=-2
| 2 |
∵M是PQ的中点,∴
|
∴r2=(x-x0)2+(y-y0)2=
| 27 |
| 4 |
所以过点P,Q,O的圆的方程为(x+
| ||
| 2 |
| 5 |
| 2 |
| 27 |
| 4 |
点评:本题考查利用导数研究抛物线切线的方程,考查向量知识,考查圆的方程,解题的关键是直线与抛物线联立,确定圆的圆心的坐标与半径.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
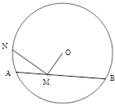 (2012•广东模拟)(几何证明选讲选做题)如图,点M为⊙O的弦AB上的一点,连接MO.MN⊥OM,MN交圆于N,若MA=2,MB=4,则MN=
(2012•广东模拟)(几何证明选讲选做题)如图,点M为⊙O的弦AB上的一点,连接MO.MN⊥OM,MN交圆于N,若MA=2,MB=4,则MN=