题目内容
（2013•南通二模）函数f（x）=（x-1）sinπx-1（-1＜x＜3）的所有零点之和为
4
4
．分析：画出图象，可看出交点的个数，并利用对称性即可求出．
解答：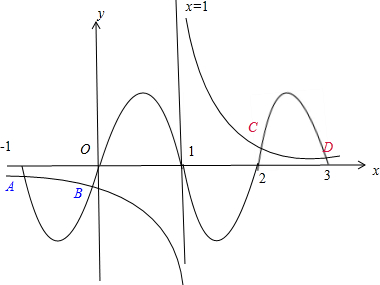
解：由（x）=（x-1）sinπx-1=0（-1＜x＜3）
可得sinπx=
令g（x）=sinπx，h（x）=
，（-a＜x＜3）
则g（x），h（x）都是关于（1，0）点对称的函数
故交点关于（1，0）对称
又根据函数图象可知，函数g（x）与h（x）有4个交点，分别记为A，B，C，D
则xA+xB+xC+xD=4
故答案为：4
解：由（x）=（x-1）sinπx-1=0（-1＜x＜3）可得sinπx=
| 1 |
| x-1 |
令g（x）=sinπx，h（x）=
| 1 |
| x-1 |
则g（x），h（x）都是关于（1，0）点对称的函数
故交点关于（1，0）对称
又根据函数图象可知，函数g（x）与h（x）有4个交点，分别记为A，B，C，D
则xA+xB+xC+xD=4
故答案为：4
点评：熟练掌握数形结合的思想方法和函数的对称性是解题的关键
练习册系列答案
王后雄学案教材完全解读系列答案
相关题目
（2013•南通二模）某篮球运动员在7天中进行投篮训练的时间（单位：分钟）用茎叶图表示（如图），图中左列表示训练时间的十位数，右列表示训练时间的个位数，则该运动员这7天的平均训练时间为