题目内容

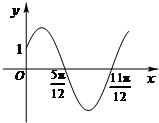精英家教网已知函数f（x）=Asin（ωx+φ）(x∈R，A＞0，ω＞0，0＜φ＜
π2
)的部分图象如图所示，求函数f（x）的解析式．
分析：由周期可得ω的值，代点(
5π
12
，0)结合φ的范围可得φ值，然后代点（0，1）可得A值，进而可得函数解析式．
解答：解：依题意知，周期T=2(
11π
12
-
5π
12
)=π，
∴ω=
2π
T
=2．
∵点(
5π
12
，0)在函数图象上，
∴Asin(2×
5π
12
+φ)=0，化简可得sin(
5π
6
+φ)=0．
又∵0＜φ＜
π
2
，
∴
5π
6
＜
5π
6
+φ＜
4π
3
，
∴
5π
6
+φ=π，解得φ=
π
6
，
又点（0，1）在函数图象上，
∴Asin
π
6
=1，A=2，
故函数f（x）的解析式为：f(x)=2sin(2x+
π
6
)
点评：本题考查三角函数解析式的求解，涉及三角函数的周期性和特殊点，属中档题．
练习册系列答案
相关题目
已知函数f（x）=
a-x2
x
+lnx  (a∈R ， x∈[
1
2
 ， 2])
（1）当a∈[-2，
1
4
)时，求f（x）的最大值；
（2）设g（x）=[f（x）-lnx]•x2，k是g（x）图象上不同两点的连线的斜率，否存在实数a，使得k≤1恒成立？若存在，求a的取值范围；若不存在，请说明理由．
（2009•海淀区二模）已知函数f（x）=a-2x的图象过原点，则不等式f(x)＞
34
的解集为
（-∞，-2）
（-∞，-2）
．
已知函数f（x）=a|x|的图象经过点（1，3），解不等式f(
2x
)＞3．
已知函数f（x）=a•2x+b•3x，其中常数a，b满足a•b≠0
（1）若a•b＞0，判断函数f（x）的单调性；
（2）若a=-3b，求f（x+1）＞f（x）时的x的取值范围．
已知函数f（x）=a-2|x|+1（a≠0），定义函数F（x）=
f(x)   ，  x＞0
-f(x) ，    x＜0
 给出下列命题：①F（x）=|f（x）|； ②函数F（x）是奇函数；③当a＜0时，若mn＜0，m+n＞0，总有F（m）+F（n）＜0成立，其中所有正确命题的序号是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网