题目内容
已知函数f(x)=ax2-2x+lnx,
(Ⅰ)若f(x)无极值点,但其导函数f′(x)有零点,求a的值;
(Ⅱ)若f(x)有两个极值点,求a的取值范围,并证明f(x)的极小值小于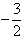 。
。
(Ⅰ)若f(x)无极值点,但其导函数f′(x)有零点,求a的值;
(Ⅱ)若f(x)有两个极值点,求a的取值范围,并证明f(x)的极小值小于
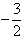 。
。 解:(Ⅰ)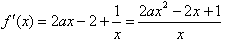 ,
,
f′(x)有零点而f(x)无极值点,
表明该零点左右f′(x)同号,故a≠0,且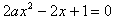 的△=0,
的△=0,
由此可得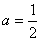 ;
;
(Ⅱ)由题意,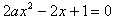 有两不同的正根,
有两不同的正根,
故△>0,a>0,解得: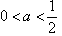 ;
;
设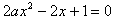 的两根为
的两根为 ,
,
因为在区间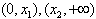 均有f′(x)>0,而在区间
均有f′(x)>0,而在区间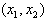 上,f′(x)<0,
上,f′(x)<0,
故x2是f(x)的极小值点,
∴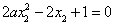 ,
,
∴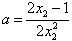 ,
,
由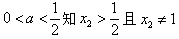 ,
,
∴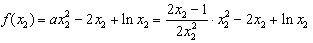
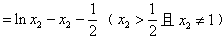 ,
,
构造函数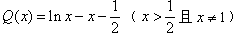 ,
,
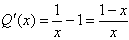 ,
,
∴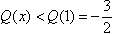 ,
,
∴f(x)的极小值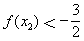 。
。
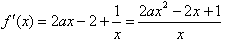 ,
,f′(x)有零点而f(x)无极值点,
表明该零点左右f′(x)同号,故a≠0,且
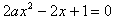 的△=0,
的△=0,由此可得
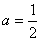 ;
;(Ⅱ)由题意,
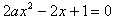 有两不同的正根,
有两不同的正根,故△>0,a>0,解得:
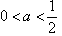 ;
;设
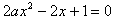 的两根为
的两根为 ,
,因为在区间
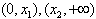 均有f′(x)>0,而在区间
均有f′(x)>0,而在区间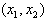 上,f′(x)<0,
上,f′(x)<0,故x2是f(x)的极小值点,
∴
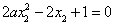 ,
,∴
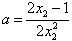 ,
,由
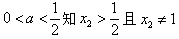 ,
,∴
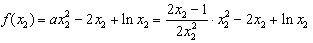
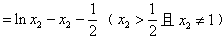 ,
,构造函数
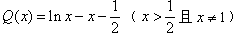 ,
,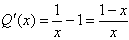 ,
,∴
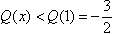 ,
,∴f(x)的极小值
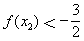 。
。
练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目