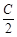题目内容
设a、b、c是三角形的边长,求证
思路分析:根据不等式的对称性,三个字母地位相同,不妨设出大小顺序,结合三角形三边之间的关系,进而应用放缩法选择适当的式子放缩变形,以达到证明目的.
证明:由不等式的对称性,不妨设a≥b≥c,则b+c-a≤c+a-b≤a+b-c,
且
∴![]() -3=
-3=![]() -1+
-1+![]() -1+
-1+![]() -1
-1
=![]() =0,
=0,
∴![]() ≥3.
≥3.
方法归纳
本题中为什么要将b+c-a与a+b-c都放缩为c+a-b呢?这是因为![]() 无法放缩.所以在运用放缩法时要注意放缩能否实现及放缩的跨度.
无法放缩.所以在运用放缩法时要注意放缩能否实现及放缩的跨度.

练习册系列答案
相关题目
设A、B、C是三角形的三个内角,下列关系恒成立的是( )
| A、cos(A+B)=cosC | ||||
| B、sin(A+B)=sinC | ||||
| C、tan(A+B)=tanC | ||||
D、sin
|
设a,b,c是三角形ABC的边长,对任意实数x,f(x)=b2x2+(b2+c2-a2)x+c2有( )
| A、f(x)=0 | B、f(x)>0 | C、f(x)≥0 | D、f(x)<0 |
 =sin
=sin