题目内容
已知椭圆 过点
过点 ,且离心率e=
,且离心率e=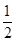 .
.
(Ⅰ)求椭圆方程;
(Ⅱ)若直线 与椭圆交于不同的两点
与椭圆交于不同的两点 、
、 ,且线段
,且线段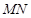 的垂直平分线过定点
的垂直平分线过定点 ,求
,求 的取值范围。
的取值范围。
(Ⅰ)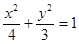 ;(Ⅱ)
;(Ⅱ)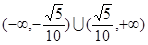 .
.
解析试题分析:(Ⅰ)由题意椭圆的离心率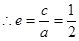
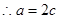
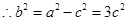
∴椭圆方程为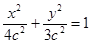 …………2分
…………2分
又点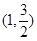 在椭圆上
在椭圆上 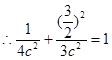
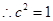 ……………4分
……………4分
∴椭圆的方程为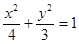 ……………6分
……………6分
(Ⅱ)设 由
由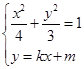
消去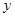 并整理得
并整理得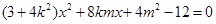 …………8分
…………8分
∵直线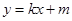 与椭圆有两个交点
与椭圆有两个交点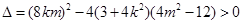 ,即
,即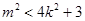
又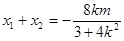
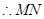 中点
中点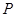 的坐标为
的坐标为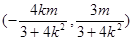 ……10分
……10分
设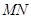 的垂直平分线
的垂直平分线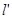 方程:
方程: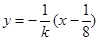
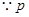 在
在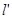 上
上 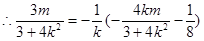 即
即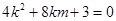
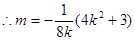 ……11分
……11分
将上式代入得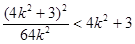
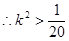
即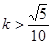 或
或
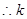 的取值范围为
的取值范围为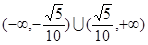 ……12分
……12分
考点:椭圆的简单性质;直线与椭圆的综合应用;中点坐标公式;直线垂直的条件。
点评:直线与圆锥曲线联系在一起的综合题在高考中多以高档题、压轴题出现,主要涉及位置关系的判定,弦长问题、最值问题、对称问题、轨迹问题等.突出考查了数形结合、分类讨论、函数与方程、等价转化等数学思想方法.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目
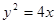 及点
及点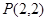 ,直线
,直线 的斜率为1且不过点P,与抛物线交于A,B两点。
的斜率为1且不过点P,与抛物线交于A,B两点。 轴上截距的取值范围;
轴上截距的取值范围; 、
、 两个岛屿,
两个岛屿, ,曾有渔船在距
,曾有渔船在距 轴,
轴, 的垂直平分线为
的垂直平分线为 轴建立平面直角坐标系。
轴建立平面直角坐标系。
 处反射信号的时间比为
处反射信号的时间比为 ,问你能否确定
,问你能否确定 ,焦点在x轴上,离心率为
,焦点在x轴上,离心率为 ,又椭圆上任一点到两焦点的距离和为
,又椭圆上任一点到两焦点的距离和为 ,过点M(0,
,过点M(0, )与x轴不垂直的直线
)与x轴不垂直的直线 交椭圆于P、Q两点.
交椭圆于P、Q两点. :
: 的左、右焦点分别为
的左、右焦点分别为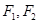 ,焦距为2,,过
,焦距为2,,过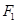 作垂直于椭圆长轴的弦长
作垂直于椭圆长轴的弦长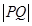 为3.
为3. 求椭圆
求椭圆 两点.并判断是否存在直线l使得
两点.并判断是否存在直线l使得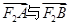 的夹角为钝角,若存在,求出l的斜率k的取值范围。
的夹角为钝角,若存在,求出l的斜率k的取值范围。 过点
过点 ,且离心率为
,且离心率为 .
. 的方程;
的方程; 为椭圆
为椭圆 是椭圆
是椭圆 分别交直线
分别交直线 于
于 两点.
两点. 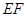 为直径的圆恒过
为直径的圆恒过 轴上的定点.
轴上的定点. ,
, 是椭圆
是椭圆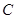 的顶点,若椭圆
的顶点,若椭圆 ,且过点
,且过点 .
.
 ,使得
,使得 ,且与椭圆
,且与椭圆 两点(异于椭圆
两点(异于椭圆 和直线
和直线 的倾斜角分别是
的倾斜角分别是 ,求证:
,求证: .
. 交抛物线
交抛物线 于A(x1,y1),B(x2,y2)两点,抛物线的顶点是
于A(x1,y1),B(x2,y2)两点,抛物线的顶点是 .
. 为定值;
为定值; 仅有一个公共点的直线
仅有一个公共点的直线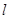 的方程.
的方程.