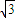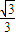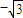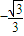题目内容
已知实数a,b均不为零,| asinα+bcosα |
| acosα-bsinα |
| π |
| 6 |
| b |
| a |
分析:把已知条件的分子分母都除以acosα得到①,然后根据β-α=
解出β的关系式,求出tanβ的值得到②,由①②相等得到
的值即可.
| π |
| 6 |
| b |
| a |
解答:解:由
=tanβ得到tanβ=
①,
又β-α=
得到β=α+
,则tanβ=tan(α+
)=
②,
由①=②得到
=
.
故答案为:
| asinα+bcosα |
| acosα-bsinα |
tanα+
| ||
1-
|
又β-α=
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
tanα+
| ||||
1-
|
由①=②得到
| b |
| a |
| ||
| 3 |
故答案为:
| ||
| 3 |
点评:此题考查学生灵活运用同角三角函数间的基本关系弦化切,灵活运用两角和的正切函数公式化简求值,是一道中档题.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
已知实数a,b均不为零,
=tanβ,且β-α=
,则
等于( )
| asinα+bcosα |
| acosα-bsinα |
| π |
| 6 |
| b |
| a |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
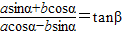 ,且
,且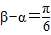 ,则
,则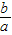 等于( )
等于( )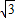
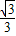
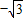

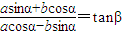 ,且
,且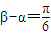 ,则
,则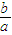 等于( )
等于( )