题目内容
等比数列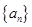 中,
中,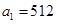 ,公比
,公比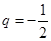 ,用
,用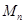 表示它的前
表示它的前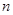 项之积,即
项之积,即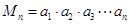 ,则数列
,则数列 中的最大项是( )
中的最大项是( )
A.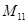 | B.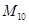 | C.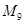 | D. |
C
解析试题分析:由已知 ,所以
,所以

要 最大,则
最大,则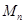 应为正,
应为正, 应为偶数
应为偶数 ,所以
,所以 ,而
,而 中必有一奇一偶,因此
中必有一奇一偶,因此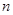 是4的倍数或
是4的倍数或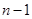 是4的倍数,
是4的倍数, ,
,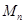 随
随 增大而增大,又
增大而增大,又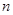 是4的倍数或
是4的倍数或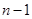 是4的倍数,当
是4的倍数,当 时,
时, 是4的倍数,此时,
是4的倍数,此时, 有最大值90,此时,
有最大值90,此时, ,所以数列
,所以数列 中的最大项是
中的最大项是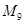 ,故选C.
,故选C.
考点:1.等比数列的通项公式;2.二次函数的图像与性质.

练习册系列答案
相关题目
在等比数列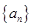 中,
中,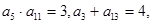 则
则 ( )
( )
A.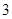 | B.3或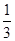 | C.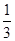 | D.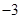 或 或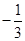 |
函数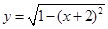 图像上存在不同的三点到原点的距离构成等比数列,则以下
图像上存在不同的三点到原点的距离构成等比数列,则以下
不可能成为公比的数是( )
A.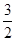 | B.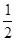 | C.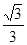 | D.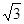 |
设一个正整数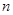 可以表示为
可以表示为
 ,其中
,其中 ,
, 中为1的总个数记为
中为1的总个数记为 ,例如
,例如 ,
, ,
, ,
, ,则
,则
A. | B. | C. | D. |
在各项均为正数的等比数列 中,若
中,若 ,则
,则 等于( )
等于( )
| A.5 | B.6 | C.7 | D.8 |
设等比数列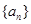 的公比为
的公比为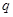 ,前
,前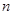 项和为
项和为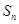 ,且
,且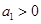 .若
.若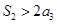 ,则
,则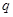 的取值范围是( )
的取值范围是( )
A.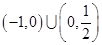 | B.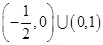 | C.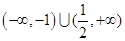 | D.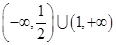 |
等比数列{an}的各项均为正数,且 ,则
,则 ( )
( )
| A.12 | B.10 | C.8 | D.2+log3 5 |
数列{an}中,已知对任意n∈N*,a1+a2+a3+…+an=3n-1,则 +
+ +
+ +…+
+…+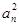 等于( )
等于( )
| A.(3n-1)2 | B. (9n-1) (9n-1) |
| C.9n-1 | D. (3n-1) (3n-1) |
 =4a1,则
=4a1,则 的最小值为( ).
的最小值为( ).