题目内容
把一根长度为7的铁丝截成3段.
(Ⅰ)如果三段的长度均为整数,求能构成三角形的概率;
(Ⅱ)如果截成任意长度的三段,求能构成三角形的概率.
(Ⅰ)如果三段的长度均为整数,求能构成三角形的概率;
(Ⅱ)如果截成任意长度的三段,求能构成三角形的概率.
分析:(Ⅰ)设构成三角形的事件为A,先求出基本事件数有4种,其中能构成三角形的情况有2种情况,从而可求能构成三角形的概率;
(Ⅱ)设把铁丝分成任意的三段,其中一段为x,第二段为y,则第三段为7-x-y,所以
,如果要构成三角形,则必须满足:
,由此求得能构成三角形的概率.
(Ⅱ)设把铁丝分成任意的三段,其中一段为x,第二段为y,则第三段为7-x-y,所以
|
|
解答: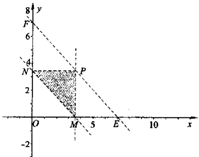 解:(Ⅰ)所有的“三段铁丝的长度”的情况共有:“1,1,5”、“1,2,4”、“1,3,3”、
解:(Ⅰ)所有的“三段铁丝的长度”的情况共有:“1,1,5”、“1,2,4”、“1,3,3”、
“2,2,3”,共计4种.
其中能构成三角形的情况有2种情况:“1,3,3”;“2,2,3”(3分)
则所求的概率是
=
.
(Ⅱ)设把铁丝分成任意的三段,其中一段为x,第二段为y,则第三段为7-x-y.
所以
,如果要构成三角形,则必须满足:
,化简可得
,
∴能构成三角形的概率为
=
.
 解:(Ⅰ)所有的“三段铁丝的长度”的情况共有:“1,1,5”、“1,2,4”、“1,3,3”、
解:(Ⅰ)所有的“三段铁丝的长度”的情况共有:“1,1,5”、“1,2,4”、“1,3,3”、“2,2,3”,共计4种.
其中能构成三角形的情况有2种情况:“1,3,3”;“2,2,3”(3分)
则所求的概率是
| 2 |
| 4 |
| 1 |
| 2 |
(Ⅱ)设把铁丝分成任意的三段,其中一段为x,第二段为y,则第三段为7-x-y.
所以
|
|
|
∴能构成三角形的概率为
| S△MNP |
| S△OEF |
| 1 |
| 4 |
点评:本题以实际问题为载体,考查概率知识的运用,解题的关键是分清是古典概型,还是几何概型,从而利用公式求解,属于中档题.

练习册系列答案
相关题目
 B.
B. C.
C.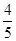 D.
D.