题目内容
(1)若lgx+lgy=1,求| 1 |
| x |
| 1 |
| y |
(2)当a>0,0≤x≤1时,讨论函数y=f(x)=-x2+2ax的最值.
分析:(1)由lgx+lgy=1可知xy的关系,代入
+
,利用基本不等式求其最小值.
(2)考查函数y=f(x)=-x2+2ax 的开口方向,对称轴方程;然后对a分类讨论,在0≤x≤1时,分别求函数y=f(x)=-x2+2ax的最值.
| 1 |
| x |
| 1 |
| y |
(2)考查函数y=f(x)=-x2+2ax 的开口方向,对称轴方程;然后对a分类讨论,在0≤x≤1时,分别求函数y=f(x)=-x2+2ax的最值.
解答:解:(1)由lgx+lgy=1可知x>0,y>0,xy=10,
所以
=
,
+
= (
+
)
=
(
+
)≥
当且仅当x=y时取等号.
+
的最小值是
(2)函数y=f(x)=-x2+2ax的对称轴为x=a,开口向下,
过(0,0)(2a,0)点,
当0<a≤
时,函数的最大值是a2,最小值是:2a-1;
当1≥a>
时,函数的最大值是a2,最小值是:0;
当a>1时,函数的最大值是2a-1,最小值是:0;
所以
| xy |
| 10 |
| 1 |
| x |
| 1 |
| y |
| 1 |
| x |
| 1 |
| y |
| ||
|
| ||
| 10 |
| ||
|
| ||
|
| ||
| 5 |
当且仅当x=y时取等号.
| 1 |
| x |
| 1 |
| y |
| ||
| 5 |
(2)函数y=f(x)=-x2+2ax的对称轴为x=a,开口向下,
过(0,0)(2a,0)点,
当0<a≤
| 1 |
| 2 |
当1≥a>
| 1 |
| 2 |
当a>1时,函数的最大值是2a-1,最小值是:0;
点评:本题考查对数的运算性质,基本不等式,函数最值的讨论,是中档题.

练习册系列答案
相关题目
现有两个命题:
(1)若lgx+lgy=lg(x+y),且不等式y>-2x+t恒成立,则t的取值范围是集合P;
(2)若函数f(x)=
,x∈(1,+∞)的图象与函数g(x)=-2x+t的图象没有交点,则t的取值范围是集合Q;
则以下集合关系正确的是( )
(1)若lgx+lgy=lg(x+y),且不等式y>-2x+t恒成立,则t的取值范围是集合P;
(2)若函数f(x)=
| x |
| x-1 |
则以下集合关系正确的是( )
| A、P?Q | B、Q?P |
| C、P=Q | D、P∩Q=∅ |
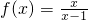 ,x∈(1,+∞)的图象与函数g(x)=-2x+t的图象没有交点,则t的取值范围是集合Q;
,x∈(1,+∞)的图象与函数g(x)=-2x+t的图象没有交点,则t的取值范围是集合Q;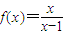 ,x∈(1,+∞)的图象与函数g(x)=-2x+t的图象没有交点,则t的取值范围是集合Q;
,x∈(1,+∞)的图象与函数g(x)=-2x+t的图象没有交点,则t的取值范围是集合Q;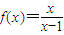 ,x∈(1,+∞)的图象与函数g(x)=-2x+t的图象没有交点,则t的取值范围是集合Q;
,x∈(1,+∞)的图象与函数g(x)=-2x+t的图象没有交点,则t的取值范围是集合Q;