题目内容
（2012•江西）观察下列事实|x|+|y|=1的不同整数解（x，y）的个数为4，|x|+|y|=2的不同整数解（x，y）的个数为8，|x|+|y|=3的不同整数解（x，y）的个数为12 …．则|x|+|y|=20的不同整数解（x，y）的个数为（ ）
分析：观察可得不同整数解的个数可以构成一个首项为4，公差为4的等差数列，则所求为第20项，可计算得结果．
解答：解：观察可得不同整数解的个数4，8，12，…可以构成一个首项为4，公差为4的等差数列，
通项公式为an=4n，则所求为第20项，所以a20=80
故选B．
通项公式为an=4n，则所求为第20项，所以a20=80
故选B．
点评：本题考查归纳推理，分寻找关系式内部，关系式与关系式之间数字的变化特征，从特殊到一般，进行归纳推理．
练习册系列答案
名校课堂系列答案
相关题目
（2012•江西）如图，已知正四棱锥S-ABCD所有棱长都为1，点E是侧棱SC上一动点，过点E垂直于SC的截面将正四棱锥分成上、下两部分．记SE=x（0＜x＜1），截面下面部分的体积为V（x），则函数y=V（x）的图象大致为（ ）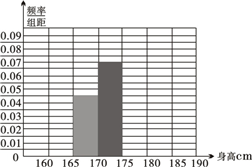
（2012•江西模拟）某省重点中学从高二年级学生中随机地抽取120名学生，测得身高情况如下表所示．