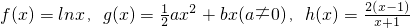题目内容
已知f(x)与g(x)分别是定义在R上奇函数与偶函数,若f(x)+g(x)=log2(x2+x+2),则f(1)等于
- A.-

- B.

- C.1
- D.2
B
分析:由题意可得:f(1)+g(1)=log24=2,f(-1)+g(-1)=log22=1,结合函数的奇偶性可得f(-1)+g(-1)=-f(1)+g(1),进而求出答案.
解答:令x=1可得f(1)+g(1)=log24=2,
令x=-1可得f(-1)+g(-1)=log22=1,
因为f(x)与g(x)分别是定义在R上奇函数与偶函数,
所以f(-1)+g(-1)=-f(1)+g(1),
所以-f(1)+g(1)=1,
所以解得f(1)= .
.
故选B.
点评:本题主要考查函数的奇偶性,以及利用函数的这一性质求函数值.
分析:由题意可得:f(1)+g(1)=log24=2,f(-1)+g(-1)=log22=1,结合函数的奇偶性可得f(-1)+g(-1)=-f(1)+g(1),进而求出答案.
解答:令x=1可得f(1)+g(1)=log24=2,
令x=-1可得f(-1)+g(-1)=log22=1,
因为f(x)与g(x)分别是定义在R上奇函数与偶函数,
所以f(-1)+g(-1)=-f(1)+g(1),
所以-f(1)+g(1)=1,
所以解得f(1)=
 .
.故选B.
点评:本题主要考查函数的奇偶性,以及利用函数的这一性质求函数值.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目