题目内容
给定椭圆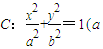 >b>0),称圆心在原点O,半径为
>b>0),称圆心在原点O,半径为 的圆是椭圆C的“伴随圆”.若椭圆C的一个焦点为
的圆是椭圆C的“伴随圆”.若椭圆C的一个焦点为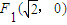 ,其短轴上的一个端点到F1的距离为
,其短轴上的一个端点到F1的距离为 .
.(1)求椭圆C的方程及其“伴随圆”方程;
(2)若倾斜角为45°的直线l与椭圆C只有一个公共点,且与椭圆C的伴随圆相交于M、N两点,求弦MN的长;
(3)点P是椭圆C的伴随圆上的一个动点,过点P作直线l1,l2,使得l1,l2与椭圆C都只有一个公共点,求证:l1⊥l2.
【答案】分析:(1)直接由椭圆C的一个焦点为 ,其短轴上的一个端点到F1的距离为
,其短轴上的一个端点到F1的距离为 ,求出,即可求椭圆C的方程及其“伴随圆”方程;
,求出,即可求椭圆C的方程及其“伴随圆”方程;
(2)先把直线方程与椭圆方程联立,利用对应的判别式为0求出,进而求出直线方程以及圆心到直线的距离;即可求弦MN的长;
(3)先对直线l1,l2的斜率是否存在分两种情况讨论,然后对每一种情况中的直线l1,l2与椭圆C都只有一个公共点进行求解即可证:l1⊥l2.(在斜率存在时,是先设直线方程,把直线与椭圆方程联立,利用斜率为对应方程的根来判断结论).
解答:解:(1)因为 ,所以b=1(12分)
,所以b=1(12分)
所以椭圆的方程为 ,
,
伴随圆的方程为x2+y2=4.(4分)
(2)设直线l的方程y=x+b,由 得4x2+6bx+3b2-3=0
得4x2+6bx+3b2-3=0
由△=(6b)2-16(3b2-3)=0得b2=4(6分)
圆心到直线l的距离为
所以 (8分)
(8分)
(3)①当l1,l2中有一条无斜率时,不妨设l1无斜率,
因为l1与椭圆只有一个公共点,则其方程为 或
或 ,
,
当l1方程为 时,此时l1与伴随圆交于点
时,此时l1与伴随圆交于点 ,
,
此时经过点 (或
(或 且与椭圆只有一个公共点的直线是y=1(或y=-1),
且与椭圆只有一个公共点的直线是y=1(或y=-1),
即l2为y=1(或y=-1),显然直线l1,l2垂直;
同理可证l1方程为 时,直线l1,l2垂直.(10分)
时,直线l1,l2垂直.(10分)
②当l1,l2都有斜率时,设点P(x,y),其中x2+y2=4,
设经过点P(x,y),与椭圆只有一个公共点的直线为y=k(x-x)+y,
由 ,消去y得到x2+3(kx+(y-kx))2-3=0,
,消去y得到x2+3(kx+(y-kx))2-3=0,
即(1+3k2)x2+6k(y-kx)x+3(y-kx)2-3=0,(12分)
△=[6k(y-kx)]2-4•(1+3k2)[3(y-kx)2-3]=0,
经过化简得到:(3-x2)k2+2xyk+1-y2=0,
因为x2+y2=4,所以有(3-x2)k2+2xyk+(x2-3)=0,(14分)
设l1,l2的斜率分别为k1,k2,因为l1,l2与椭圆都只有一个公共点,
所以k1,k2满足方程(3-x2)k2+2xyk+(x2-3)=0,
因而k1•k2=-1,即l1,l2垂直.(16分)
点评:本题主要考查椭圆的方程和几何性质,直线的方程,两点间的距离公式以及点到直线的距离公式等基础知识,考查用代数方法研究圆锥曲线的性质和数形结合的数学思想,考查解决问题的能力和运算能力.
 ,其短轴上的一个端点到F1的距离为
,其短轴上的一个端点到F1的距离为 ,求出,即可求椭圆C的方程及其“伴随圆”方程;
,求出,即可求椭圆C的方程及其“伴随圆”方程;(2)先把直线方程与椭圆方程联立,利用对应的判别式为0求出,进而求出直线方程以及圆心到直线的距离;即可求弦MN的长;
(3)先对直线l1,l2的斜率是否存在分两种情况讨论,然后对每一种情况中的直线l1,l2与椭圆C都只有一个公共点进行求解即可证:l1⊥l2.(在斜率存在时,是先设直线方程,把直线与椭圆方程联立,利用斜率为对应方程的根来判断结论).
解答:解:(1)因为
 ,所以b=1(12分)
,所以b=1(12分)所以椭圆的方程为
 ,
,伴随圆的方程为x2+y2=4.(4分)
(2)设直线l的方程y=x+b,由
 得4x2+6bx+3b2-3=0
得4x2+6bx+3b2-3=0由△=(6b)2-16(3b2-3)=0得b2=4(6分)
圆心到直线l的距离为

所以
 (8分)
(8分)(3)①当l1,l2中有一条无斜率时,不妨设l1无斜率,
因为l1与椭圆只有一个公共点,则其方程为
 或
或 ,
,当l1方程为
 时,此时l1与伴随圆交于点
时,此时l1与伴随圆交于点 ,
,此时经过点
 (或
(或 且与椭圆只有一个公共点的直线是y=1(或y=-1),
且与椭圆只有一个公共点的直线是y=1(或y=-1),即l2为y=1(或y=-1),显然直线l1,l2垂直;
同理可证l1方程为
 时,直线l1,l2垂直.(10分)
时,直线l1,l2垂直.(10分)②当l1,l2都有斜率时,设点P(x,y),其中x2+y2=4,
设经过点P(x,y),与椭圆只有一个公共点的直线为y=k(x-x)+y,
由
 ,消去y得到x2+3(kx+(y-kx))2-3=0,
,消去y得到x2+3(kx+(y-kx))2-3=0,即(1+3k2)x2+6k(y-kx)x+3(y-kx)2-3=0,(12分)
△=[6k(y-kx)]2-4•(1+3k2)[3(y-kx)2-3]=0,
经过化简得到:(3-x2)k2+2xyk+1-y2=0,
因为x2+y2=4,所以有(3-x2)k2+2xyk+(x2-3)=0,(14分)
设l1,l2的斜率分别为k1,k2,因为l1,l2与椭圆都只有一个公共点,
所以k1,k2满足方程(3-x2)k2+2xyk+(x2-3)=0,
因而k1•k2=-1,即l1,l2垂直.(16分)
点评:本题主要考查椭圆的方程和几何性质,直线的方程,两点间的距离公式以及点到直线的距离公式等基础知识,考查用代数方法研究圆锥曲线的性质和数形结合的数学思想,考查解决问题的能力和运算能力.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目
 >b>0),称圆心在原点O,半径为
>b>0),称圆心在原点O,半径为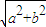 的圆是椭圆C的“伴随圆”.若椭圆C的一个焦点为
的圆是椭圆C的“伴随圆”.若椭圆C的一个焦点为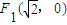 ,其短轴上的一个端点到F1的距离为
,其短轴上的一个端点到F1的距离为 .
.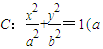 >b>0),称圆心在原点O,半径为
>b>0),称圆心在原点O,半径为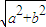 的圆是椭圆C的“准圆”.若椭圆C的一个焦点为
的圆是椭圆C的“准圆”.若椭圆C的一个焦点为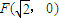 ,其短轴上的一个端点到F的距离为
,其短轴上的一个端点到F的距离为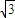 .
.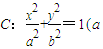 >b>0),称圆心在原点O,半径为
>b>0),称圆心在原点O,半径为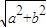 的圆是椭圆C的“准圆”.若椭圆C的一个焦点为
的圆是椭圆C的“准圆”.若椭圆C的一个焦点为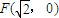 ,其短轴上的一个端点到F的距离为
,其短轴上的一个端点到F的距离为 .
. >b>0),称圆心在原点O,半径为
>b>0),称圆心在原点O,半径为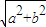 的圆是椭圆C的“准圆”.若椭圆C的一个焦点为
的圆是椭圆C的“准圆”.若椭圆C的一个焦点为 ,其短轴上的一个端点到F的距离为
,其短轴上的一个端点到F的距离为 .
.