Question

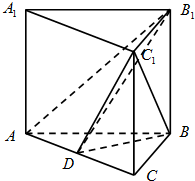正三棱柱ABC-A₁B₁C₁中，AB=2，AA1=

2

，D是AC中点
（Ⅰ）求三棱锥B₁-BDC₁的体积；
（Ⅱ） 证明：AB₁⊥BC₁．

Answer 1

分析：（1）正三棱柱ABC-A₁B₁C₁中，由AB=2，AA1=

2

，D是AC中点，能求出三棱锥D-B₁BC₁的高，由此利用等积法能求出三棱锥B₁-BDC₁的体积．
（2）分别取BB₁、B₁C₁、AB、BC的中点E，F，O，G，连接EF，OF，OE，GF，GO，由EF

∥

.

1

2

BC=

6

2

，OE

∥

.

1

2

AB1=

6

2

，OF=

3

，得到∠OEF是异面直线AB₁和BC₁所成的角或所成角的补角．由此利用余弦定理能证明AB₁⊥BC₁．

解答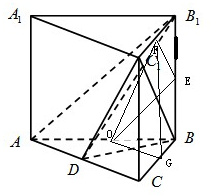：（1）解：正三棱柱ABC-A₁B₁C₁中，
∵AB=2，AA1=

2

，D是AC中点，
∴S△B1BC1=

1

2

×2×

2

=

2

，
三棱锥D-B₁BC₁的高h=

1

2

×

22-12

=

3

2

，
∴三棱锥B₁-BDC₁的体积
VB1-BDC1=VD-B1BC1=

1

3

×

2

×

3

2

=

6

6

．…（6分）
（2）证明：分别取BB₁、B₁C₁、AB、BC的中点E，F，O，G，
连接EF，OF，OE，GF，GO，
则EF

∥

.

1

2

BC=

6

2

，OE

∥

.

1

2

AB1=

6

2

，OF=

OG2+GF2

=

3

，
∴∠OEF是异面直线AB₁和BC₁所成的角或所成角的补角．
∵cos∠OEF=

( 6 2 )2+( 6 2 )2-( 3 )2

2× 6 2 × 6 2

=0，
∴∠OEF=90°，
∴AB₁⊥BC₁．…（12分）

点评：本题考查三棱锥的体积的求法，考查异面直线垂直的证明，解题时要认真审题，注意等积法和余弦定理的合理运用．