题目内容
已知 同时满足下列条件:
同时满足下列条件:
① ;②
;② .则实数
.则实数 的取值范围 .
的取值范围 .

解析试题分析:① 说明给定一个
说明给定一个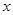 的值,
的值, 中至少一个的值小于0.对
中至少一个的值小于0.对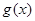 ,当
,当 时
时 ;当
;当 时
时 .所以当
.所以当 时必有
时必有 ,从而
,从而 .由
.由 得
得 .由
.由 得
得 .当
.当 时,
时, 的解为
的解为 或
或 ,此时应有
,此时应有 .当
.当 时,
时, 的解为
的解为 或
或 ,此时应有
,此时应有 ,所以
,所以 .
. 时
时 ,此时
,此时 ,不满足②.当
,不满足②.当 时,都满足②.故实数
时,都满足②.故实数 的取值范围是
的取值范围是 .
.
考点:函数与不等式.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
设xy<0,x,y∈R,那么下列结论正确的是( )
| A.|x+y|<|x-y| | B.|x-y|<|x|+|y| |
| C.|x+y|>|x-y| | D.|x-y|<||x|-|y|| |
若关于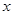 的不等式
的不等式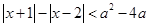 有实数解,则实数
有实数解,则实数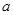 的取值范围为( )
的取值范围为( )
A.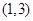 | B. | C.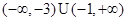 | D. |
 恒成立,则实数a的取值范围为 ________;
恒成立,则实数a的取值范围为 ________;  的解集是
的解集是  使得
使得 成立,则实数
成立,则实数 的取值范围为 .
的取值范围为 . ,则不等式f(x)-x≤2的解集是________.
,则不等式f(x)-x≤2的解集是________.