题目内容
已知在三棱锥S—ABC中,SA=SB=SC,∠ASB=∠ASC=60°,∠BSC=90°,求证：平面ABC⊥平面BSC.
思路解析：要证明面面垂直,可以考虑利用面面垂直的定义,去证明这两个平面所成的二面角是直二面角;也可以根据面面垂直的判定定理来证明.
证明：取BC的中点D，连结AD、SD.
∵SA=SB=SC,∠ASB=∠ASC=60°，∴△ASB≌△ASC,且均为等边三角形,AB=AC=SB=SC.
∴AD⊥BC，SD⊥BC，∠ADS是二面角ABCS的平面角.
不妨设SA=1,因为∠BSC=90°，所以SD=
.由△SBC≌△ABC,知AD=SD=
，AS2=AD2+SD2，∠ADS=90°,即二面角ABCS是直角,所以平面ABC⊥平面BSC.
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
：
：
；
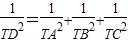（注：S△ABC表示△ABC的面积）