题目内容
已知抛物线y2=2px(p>0),过动点M(a,0)且斜率为1的直线l与该抛物线交于不同的两点A、B.(1)若|AB|≤2p,求a的取值范围;
(2)若线段AB的垂直平分线交AB于Q,交x轴于点N,试求Rt△MNQ的面积.
解:(1)直线l的方程为y=x-a,将y=x-a代入y2=2px,得x2-2(a+p)x+a2=0. 设直线l与抛物线两个不同交点的坐标为A(x1,y1)、B(x2,y2),则 ∴|AB|= 由0<|AB|≤2p,8p(p+2a)>0,解得- (2)设Q(x3,y3),由中点坐标公式,得x3= y3= ∴|QM|2=(a+p-a)2+(p-0)2=2p2. 又△MNQ为等腰直角三角形,∴S△MNQ=
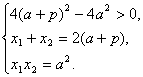
![]() .
.![]() <a≤-
<a≤-![]() .
.![]() =a+p,
=a+p,![]() =p,
=p,![]() |QM|2=p2.
|QM|2=p2.
 练习册系列答案
练习册系列答案
星火英语SPARK系列答案
单元检测新疆电子音像出版社系列答案
新课标数学口算天天练系列答案
恒基中考备战策略系列答案

快乐小博士小考总动员系列答案
百分阅读系列答案

经纶学典考点解析系列答案
备考金卷智能优选卷系列答案
相关题目