题目内容
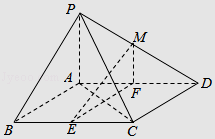
【题目】如图1,在直角梯形ABCD中,AB∥DC,∠BAD=90°,AB=AD= ![]() CD=1,如图2,将△ABD沿BD折起来,使平面ABD⊥平面BCD,设E为AD的中点,F为AC上一点,O为BD的中点.
CD=1,如图2,将△ABD沿BD折起来,使平面ABD⊥平面BCD,设E为AD的中点,F为AC上一点,O为BD的中点. 
(Ⅰ)求证:AO⊥平面BCD;、
(Ⅱ)若三棱锥A﹣BEF的体积为 ![]() ,求二面角A﹣BE﹣F的余弦值的绝对值.
,求二面角A﹣BE﹣F的余弦值的绝对值.
【答案】证明:在图1中,取CD的中点E,连结BE, ∵AB∥DC,∠BAD=90°,AB=AD= ![]() CD=1,
CD=1,
∴BE=DE=CE=1,BE⊥CD,
∴∠DBE=∠CBE=45°,
∴BC⊥BD,
又平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,BC平面BCD,
∴BC⊥平面ABD,∵AO平面ABD,
∴AO⊥BC,
∵AB=AD,O是BD的中点,
∴AO⊥BD,又BD∩BC=B,BD平面BCD,BC平面BCD,
∴AO⊥平面BCD.
(II)解:设F到平面ABD的距离为h,
则VA﹣BEF=VF﹣ABE= ![]() =
= ![]() =
= ![]() ,∴h=
,∴h= ![]() .
.
∴CF= ![]() CA.
CA.
由(I)可知OE⊥BD,以O为原点,以OD,OE,OA为坐标轴建立空间直角坐标系O﹣xyz,
则A(0,0, ![]() ),B(﹣
),B(﹣ ![]() ,0,0),E(
,0,0),E( ![]() ,0,
,0, ![]() ),C(﹣
),C(﹣ ![]() ,
, ![]() ,0),
,0),
∴ ![]() =(
=( ![]() ,0,
,0, ![]() ),
), ![]() =(0,
=(0, ![]() ,0),
,0), ![]() =(
=( ![]() ,﹣
,﹣ ![]() ,
, ![]() ),
),
∴ ![]() =
= ![]() =
= ![]() =(
=( ![]() ,
, ![]() ,
, ![]() ),
),
设平面BEF的法向量为 ![]() =(x,y,z),则
=(x,y,z),则  ,
,
∴  ,令x=1得
,令x=1得 ![]() =(1,
=(1, ![]() ,﹣3),
,﹣3),
∵BC⊥平面ABD,∴ ![]() =(0,
=(0, ![]() ,0)是平面ABD的一个法向量,
,0)是平面ABD的一个法向量,
∴cos< ![]() >=
>=  =
=  =
= ![]() .
.
∴二面角A﹣BE﹣F的余弦值的绝对值为 ![]() .
.
【解析】(I)由面面垂直可得BC⊥平面ABD,故而BC⊥AO,结合AO⊥BD即可得出AO⊥平面BCD;(II)根据棱锥的体积得出F的位置,建立空间坐标系,求出两平面的法向量,则两法向量的夹角的余弦的绝对值即为所求.
【考点精析】关于本题考查的直线与平面垂直的判定,需要了解一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能得出正确答案.

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案