Question

【题目】已知函数f（x）= sinxcosx+cos2x
（I）求函数f（x）的最小正周期；
（II）若﹣ ＜α＜0，f（α）= ，求sin2α的值．

Answer 1

【答案】解：（I）∵函数f（x）= sinxcosx+cos2x= sin2x+ =sin（2x+ ）+ ， ∴函数f（x）的最小正周期为 =π．
（II）若﹣ ＜α＜0，则2α+ ∈（﹣ ， ），
∴f（α）=sin（2α+ ）+ = ，∴sin（2α+ ）= ，∴2α+ ∈（0， ），
∴cos（2α+ ）= = ，
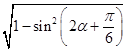∴sin2α=sin（2α+ ﹣ ）=sin（2α+ ）cos ﹣cos（2α+ ）sin = ﹣ = ．
【解析】（I）利用三角恒等变换化简函数的解析式，再利用正弦函数的周期性，得出结论．（II）由条件求得sin（2α+ ）的值以及2α+ 的范围，可得cos（2α+ ）的值，再根据sin2α=sin（2α+ ﹣ ），利用两角差的正弦公式，求得sin2α的值．