Question

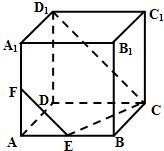
如图所示，在正方体ABCD—A₁B₁C₁D₁中，E、F分别是相邻两侧面BCC₁B₁及CDD₁C₁的中心.

（1）判断A₁E和B₁F的位置关系；

（2）求A₁E和B₁F所成角的大小.

Answer 1

解析：（1）∵B₁F平面B₁D₁C，E∈平面B₁D₁C，且EB₁F,又A₁平面B₁D₁C，∴A₁E与B₁F是异面直线.?

（2）设a为棱长，在平面B₁D₁C中，作EG∥B₁F交CD₁于G，连结A₁G，在Rt△A₁B₁E中，A₁E²=a²;在△B₁D₁C中，EG=B₁F=a;在Rt△A₁D₁G中，A₁G²=a².?

则在△A₁EG中，由余弦定理得cos∠A₁EG=-.?

∵异面直线所成角的范围是（0°,90°］,?

∴A₁E和B₁F所成角的大小为?

π-arccos(-)=arccos.