题目内容
函数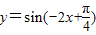 的单调递增区间是( )
的单调递增区间是( )A.
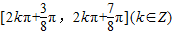
B.
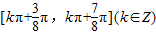
C.
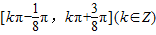
D.
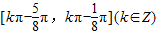
【答案】分析:本题即求函数y=sin(2x-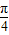 )的减区间,令 2kπ+
)的减区间,令 2kπ+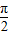 ≤2x-
≤2x-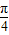 ≤2kπ+
≤2kπ+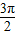 ,k∈z,求得x的范围,可得所求.
,k∈z,求得x的范围,可得所求.
解答:解:由于函数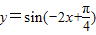 =-sin(2x-
=-sin(2x-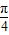 ),故函数
),故函数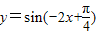 的单调递增区间,
的单调递增区间,
即函数y=sin(2x-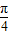 )的减区间.
)的减区间.
令 2kπ+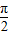 ≤2x-
≤2x-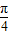 ≤2kπ+
≤2kπ+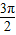 ,k∈z,求得kπ+
,k∈z,求得kπ+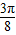 ≤x≤kπ+
≤x≤kπ+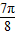 ,
,
故所求的函数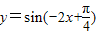 的单调递增区间是
的单调递增区间是  ,
,
故选B.
点评:本题主要考查复合三角函数的单调性,体现了转化的数学思想,属于中档题.
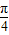 )的减区间,令 2kπ+
)的减区间,令 2kπ+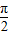 ≤2x-
≤2x-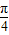 ≤2kπ+
≤2kπ+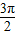 ,k∈z,求得x的范围,可得所求.
,k∈z,求得x的范围,可得所求.解答:解:由于函数
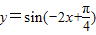 =-sin(2x-
=-sin(2x-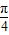 ),故函数
),故函数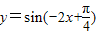 的单调递增区间,
的单调递增区间,即函数y=sin(2x-
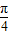 )的减区间.
)的减区间.令 2kπ+
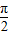 ≤2x-
≤2x-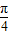 ≤2kπ+
≤2kπ+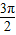 ,k∈z,求得kπ+
,k∈z,求得kπ+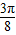 ≤x≤kπ+
≤x≤kπ+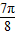 ,
,故所求的函数
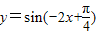 的单调递增区间是
的单调递增区间是  ,
,故选B.
点评:本题主要考查复合三角函数的单调性,体现了转化的数学思想,属于中档题.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目