题目内容
已知等差数列 的前
的前 项和为
项和为 ,且
,且 .
.
(I)求数列 的通项公式;
的通项公式;
(II)设等比数列 ,若
,若 ,求数列
,求数列 的前
的前 项和
项和
(Ⅲ)设 ,求数列
,求数列 的前
的前 项和
项和
【答案】
(Ⅰ) ;(Ⅱ)
;(Ⅱ) ;(Ⅲ)
;(Ⅲ) .
.
【解析】
试题分析:(Ⅰ)两种思路,一是根据等差数列的通项公式、求和公式,建立 的方程组;
的方程组;
二是利用等差数列的性质,由 ,得
,得 ,
,
结合 ,确定
,确定 .
.
(Ⅱ)由(I得 ,
, ,得到公比
,得到公比 ,
,  ,应用等比数列的求和公式计算.
,应用等比数列的求和公式计算.
(Ⅲ)由(Ⅰ)知, . 从而得到
. 从而得到 ,应用“裂项相消法”求和.
,应用“裂项相消法”求和.
该题综合考查等差数列、等比数列的基础知识,以及数列求和的方法,较为典型.
试题解析:(Ⅰ)法一: 解得
解得 (2分)
(2分)
 (4分)
(4分)
法二:由 ,得
,得 ,所以
,所以 .
(2分)
.
(2分)
又因为 ,所以公差
,所以公差 .
(3分)
.
(3分)
从而 .
(4分)
.
(4分)
(Ⅱ)由上可得 ,
, ,所以公比
,所以公比 ,
,
从而, (6分)
(6分)
所以. (8分)
(8分)
(Ⅲ)由(Ⅰ)知, .
.
∴ 10分
10分

 (12分)
(12分)
考点:等差数列、等比数列的通项公式及求和公式,“裂项相消法”求和.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
 的公差是
的公差是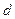 ,
, 是该数列的前
是该数列的前 项和.
项和. 表示
表示 ,其中
,其中 、
、
 ,求
,求 项的和分别为
项的和分别为
 ,试将问题(1)推广,探究相应的结论. 若能证明,则给出你的证明并求解以下给出的问题;若无法证明,则请利用你的研究结论和另一种方法计算以下给出的问题,从而对你猜想的可靠性作出自己的评价.问题:“已知等差数列
,试将问题(1)推广,探究相应的结论. 若能证明,则给出你的证明并求解以下给出的问题;若无法证明,则请利用你的研究结论和另一种方法计算以下给出的问题,从而对你猜想的可靠性作出自己的评价.问题:“已知等差数列 项和
项和 ,前
,前 项和
项和 ,求数列
,求数列 .”
.” 的前
的前 项和为
项和为 ,
,
 与前
与前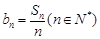 求证:数列
求证:数列 中任意不同的三项都不可能成为等比数列.
中任意不同的三项都不可能成为等比数列. 的前
的前 项和为
项和为 ,且满足
,且满足 ,则数列
,则数列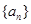 的前
的前 项和为
项和为 ,且
,且 ,
, .
. ,求证:数列
,求证:数列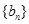 是等比数列,并求其前
是等比数列,并求其前