题目内容
下列命题中为真命题的是
- A.若b2=ac,则a,b,c成等比数列
- B.?x∈R,使得
 成立
成立 - C.若向量
 ,
, 满足
满足 ,则
,则 或
或
- D.若a<b,则
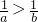
B
分析:对于A:可以举一个反例,满足b2=ac,但a、b、c不成等比数列;对于B:根据正弦型函数的值域,我们可以判定它的真假;对于C:利用向量垂直的条件进行判断;对于D:根据不等式的性质即可进行判断.
解答:A:若b=0,a=2,c=0,满足b2=ac,但a、b、c显然不成等比数列,故错;
B:∵sinx+cosx= sin(x+
sin(x+ )∈[-
)∈[- ,
, ],而
],而 ∈[-
∈[- ,
, ],故B正确;
],故B正确;
C:若向量 ,
, 满足
满足 ,则
,则 ⊥
⊥ ,不一定有:
,不一定有: 或
或 ,故C错;
,故C错;
D:若a<b,a<0,b>0,则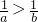 不正确.故D错.
不正确.故D错.
故选B.
点评:本题主要考查特称命题、向量垂直的条件、不等式的性质、等比数列的等比中项的性质和充要条件的判断.解题的关键应用a,b,c成等比数列时,一定要考虑a,b,c都等于0的特殊情况.
分析:对于A:可以举一个反例,满足b2=ac,但a、b、c不成等比数列;对于B:根据正弦型函数的值域,我们可以判定它的真假;对于C:利用向量垂直的条件进行判断;对于D:根据不等式的性质即可进行判断.
解答:A:若b=0,a=2,c=0,满足b2=ac,但a、b、c显然不成等比数列,故错;
B:∵sinx+cosx=
 sin(x+
sin(x+ )∈[-
)∈[- ,
, ],而
],而 ∈[-
∈[- ,
, ],故B正确;
],故B正确;C:若向量
 ,
, 满足
满足 ,则
,则 ⊥
⊥ ,不一定有:
,不一定有: 或
或 ,故C错;
,故C错;D:若a<b,a<0,b>0,则
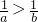 不正确.故D错.
不正确.故D错.故选B.
点评:本题主要考查特称命题、向量垂直的条件、不等式的性质、等比数列的等比中项的性质和充要条件的判断.解题的关键应用a,b,c成等比数列时,一定要考虑a,b,c都等于0的特殊情况.

练习册系列答案
相关题目
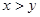 ,则
,则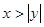 ”的逆命题
”的逆命题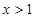 ,则
,则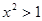 ”的否命题
”的否命题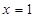 ,则
,则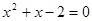 ”的否命题
”的否命题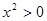 ,则
,则