题目内容
已知O为平面直角坐标系的原点,F2为双曲线
-
=1(a>0,b>0)的右焦点,若该双曲线的右支上存在一点使得|PO|=|PF2|,则该双曲线离心率的范围是
| x2 |
| a2 |
| y2 |
| b2 |
[2,+∞)
[2,+∞)
.分析:设P点的横坐标为x,过点P作x轴的垂线,根据|PO|=|PF2|,得出垂足H是OF2的中点,再结合P在双曲线右支确定x的范围,进而根据x的范围确定e的范围.
解答: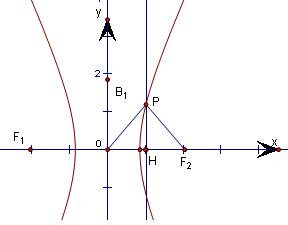 解:设P点的横坐标为x
解:设P点的横坐标为x
过点P作x轴的垂线,根据|PO|=|PF2|,得出垂足H是OF2的中点,
所以x=
,
∵P在双曲线右支
∴x≥a,
得到
≥a,⇒
≥2
∴e的范围为[2,+∞),
故答案为:[2,+∞).
 解:设P点的横坐标为x
解:设P点的横坐标为x过点P作x轴的垂线,根据|PO|=|PF2|,得出垂足H是OF2的中点,
所以x=
| c |
| 2 |
∵P在双曲线右支
∴x≥a,
得到
| c |
| 2 |
| c |
| a |
∴e的范围为[2,+∞),
故答案为:[2,+∞).
点评:本题主要考查了双曲线的简单性质.考查了双曲线中平面几何性质的灵活运用.属于基础题.

练习册系列答案
相关题目
 [选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
[选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.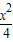 +
+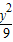 =1在M-1的作用下的新曲线的方程.
=1在M-1的作用下的新曲线的方程.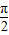 ),若直线l过点P,且倾斜角为
),若直线l过点P,且倾斜角为 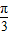 ,圆C以M为圆心、4为半径.
,圆C以M为圆心、4为半径.