Question

设P为椭圆

x2

4

+y2=1上任意一点，O为坐标原点，F为椭圆的左焦点，点M满足

OM

=

1

2

(

OP

+

OF

)，则|

OM

|+|

MF

|=

 

．

Answer 1

分析：先由点M满足

OM

=

1

2

(

OP

+

OF

)，得出M为FP中点，然后根据c²=a²-b²，求出c的值即可．

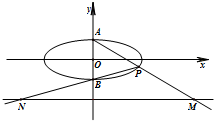
解答：解：令椭圆的右焦点为F₂，以OP、OF为邻边作平行四边形OPAF．
由平行四边形法则，有：

OA

=

OP

+

OF

，
而点M满足

OM

=

1

2

(

OP

+

OF

)，
∴

OA

=2

OM

，
∴M是OA的中点．
∵OPAF是平行四边形，
∴OA、PF互相平分，又M是OA的中点，
∴M是PF的中点，
∴MF=

1

2

PF．
显然，由椭圆方程可知：原点O是椭圆的中心，
∴O是FF₂的中点．
∵M、O分别是PF、FF₂的中点，
∴OM是△PFF₂的中位线，
∴OM=

1

2

PF₂．
由MF=

1

2

PF、OM=OM=

1

2

PF₂，
得：OM+MF=

1

2

（PF+PF₂）
由椭圆定义，有：PF+PF2=2a=2×2=4，
∴OM+MF=2．
∴|

OM

|+|

MF

|=OM+MF=2．
故答案为：2

点评：本题考查了椭圆的性质，得出|

OM

|+|

MF

|=

OF

是解题的关键，属于基础题．