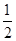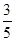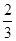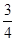题目内容
在某一试验中事件A出现的概率为 ,则在
,则在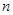 次试验中
次试验中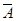 出现
出现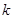 次的概率为( )
次的概率为( )
A.1-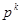 | B.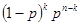 | C.1-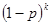 | D.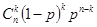 |
D
解析试题分析:根据题意,由对立事件的意义,可得n次试验中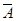 出现k次,则A出现(n-k)次;进而由n次独立重复试验中恰好发生k次的概率公式,计算可得答案.解:根据题意,在n次试验中
出现k次,则A出现(n-k)次;进而由n次独立重复试验中恰好发生k次的概率公式,计算可得答案.解:根据题意,在n次试验中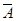 出现k次,则A出现(n-k)次;根据n次独立重复试验中恰好发生k次的概率公式可得其概率
出现k次,则A出现(n-k)次;根据n次独立重复试验中恰好发生k次的概率公式可得其概率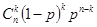 ,故答案为:D.
,故答案为:D.
考点:n次独立重复试验
点评:本题考查n次独立重复试验中恰好发生k次的概率公式的运用,解题时注意结合对立事件的意义,分析出n次试验中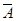 出现k次,则A出现(n-k)次;是解题的关键
出现k次,则A出现(n-k)次;是解题的关键

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
一个口袋中装有2个白球和3个黑球,则先摸出一个白球后放回,再摸出一个白球的概率是( )
A.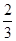 | B.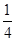 | C.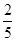 | D.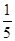 |
若 是离散型随机变量,
是离散型随机变量,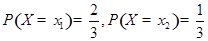 ,且
,且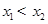 ,又已知
,又已知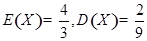 ,则
,则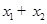 的值为( )
的值为( )
A.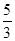 | B.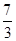 | C. | D.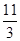 |
设随机变量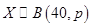 ,且
,且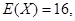 则
则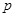 等于( )
等于( )
A.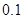 | B.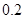 | C.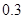 | D.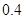 |
甲袋内装有2个红球和3个白球,乙袋内装有1个红球和
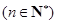 个白球.现分别从甲、乙两袋中各取1个球,若将事件“取出的2个球恰为同色”发生的概率记为
个白球.现分别从甲、乙两袋中各取1个球,若将事件“取出的2个球恰为同色”发生的概率记为 .则以下关于函数
.则以下关于函数
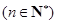 的判断正确的是
的判断正确的是
A. 有最小值,且最小值为 有最小值,且最小值为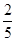 | B. 有最大值,且最大值为 有最大值,且最大值为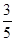 |
C. 有最小值,且最小值为 有最小值,且最小值为 | D. 有最大值,且最大值为 有最大值,且最大值为 |







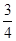


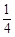


 ,则方差
,则方差 ( )
( ) B.
B. C.
C. D.
D.