题目内容
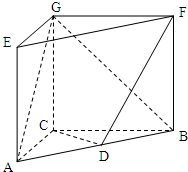如图，在三棱柱ABC-EFG中，GC⊥平面ABC，AC=3，BC=4，AB=5点D是的AB中点（1）求证：AG∥平面CDF；
（2）求证：AG⊥BC．
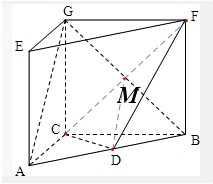
分析：（1）连接连接CF交BG于点M，连接MD，则MD为△ABG的中位线．从而MD∥AG．根据直线与平面平行的判定定理可得AG∥平面CDF
（2）根据直线与平面垂直的判定定理证明BC⊥平面ACGE，即可得到AG⊥BC．
（2）根据直线与平面垂直的判定定理证明BC⊥平面ACGE，即可得到AG⊥BC．
解答：证明：（1）如图，连接CF交BG于点M，
则点M为线段BG的中点．
连接MD
∵D是的AB中点
∴
MD为△ABG的中位线
∴MD∥AG
又∵MD?平面CDF
AG?平面CDF
∴AG∥平面CDF
（2）∵在三棱柱ABC-EFG中，GC⊥平面ABC
BC?平面ABC
∴BC⊥GC
∵AC=3，BC=4，AB=5
∴△ABC为直角三角形
∴BC⊥AC
又∵AC∩GC=C
∴BC⊥平面ACGE
而AG?平面ACGE
∴AG⊥BC
则点M为线段BG的中点．
连接MD
∵D是的AB中点
∴
MD为△ABG的中位线∴MD∥AG
又∵MD?平面CDF
AG?平面CDF
∴AG∥平面CDF
（2）∵在三棱柱ABC-EFG中，GC⊥平面ABC
BC?平面ABC
∴BC⊥GC
∵AC=3，BC=4，AB=5
∴△ABC为直角三角形
∴BC⊥AC
又∵AC∩GC=C
∴BC⊥平面ACGE
而AG?平面ACGE
∴AG⊥BC
点评：本题考查直线与平面平行的判定定理以及直线与平面垂直的判定定理的应用．属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
如图，在三棱柱ABC-A'B'C'中，若E、F分别为AB、AC的中点，平面EB'C'F将三棱柱分成体积为V1、V2的两部分，那么V1：V2为（ ）| A、3：2 | B、7：5 | C、8：5 | D、9：5 |
如图，在三棱柱ABC-A1B1C1中，AA1⊥平面ABC，A1A=AC=2，BC=1，AB=
如图，在三棱柱ABC-A1B1C1中，四边形A1ABB1为菱形，∠A1AB=60°，四边形BCC1B1为矩形，若AB⊥BC且AB=4，BC=3
（2013•通州区一模）如图，在三棱柱ABC-A1B1C1中，CC1⊥底面ABC，AC=BC=2，AB=2
如图，在三棱柱ABC-A1B1C1中，AA1⊥面ABC，AC⊥BC，E分别在线段B1C1上，B1E=3EC1，AC=BC=CC1=4．