题目内容
已知等差数列 前
前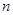 项和为
项和为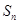 ,且
,且 ,则
,则 的值为
的值为
| A.13 | B.26 | C.8 | D.162 |
A
解析试题分析:根据题意,由于等差数列 前
前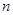 项和为
项和为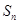 ,且
,且 ,那么根据数列的等差中项性质可知,
,那么根据数列的等差中项性质可知, ,故答案为13,选A.
,故答案为13,选A.
考点:等差数列
点评:主要是考查了等差数列的通项公式和求和的运用,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设等差数列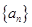 满足
满足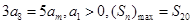 ,则m的值为 ( )
,则m的值为 ( )
A. | B.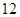 | C. | D.26 |
在 角
角 的对边分别为
的对边分别为 ,若
,若 成等差数列,则
成等差数列,则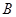 等于( )
等于( )
A. | B. | C. | D. |
已知数列 是等差数列,若
是等差数列,若 ,则数列
,则数列 的公差等于
的公差等于
| A.1 | B.3 | C.5 | D.6 |
已知等差数列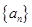 满足
满足 ,若
,若 ,则
,则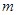 为
为
A. | B. | C. | D. |
类比“等差数列的定义”给出一个新数列“等和数列的定义”是( )
| A.连续两项的和相等的数列叫等和数列 |
| B.从第二项起,以后每一项与前一项的差都不相等的数列叫等和数列 |
| C.从第二项起,以后每一项与前一项的和都相等的数列叫等和数列 |
| D.从第一项起,以后每一项与前一项的和都相等的数列叫等和数列 |
已知{an}为等差数列, ,则
,则 等于( ).
等于( ).
| A.4 | B.5 | C.6 | D.7 |
已知数列 为等差数列且
为等差数列且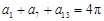 ,则
,则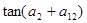 的值为( )
的值为( )
A.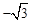 | B.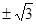 | C.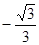 | D.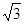 |
等差数列{an}和{bn}的前n项和分别为Sn和Tn,且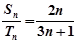 ,则
,则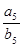 ( )
( )
A.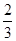 | B.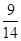 | C.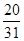 | D.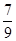 |