题目内容
已知a,b为实数,a>2,函数f(x)=|lnx-
|+b,若f(1)=e+1,f(2)=
-ln2+1.
(1)求实数a,b;
(2)求函数f(x)在[1,e2]上的取值范围;
(3)若实数c、d满足c≥d,cd=1,求f(c)+f(d)的最小值.
| a |
| x |
| e |
| 2 |
(1)求实数a,b;
(2)求函数f(x)在[1,e2]上的取值范围;
(3)若实数c、d满足c≥d,cd=1,求f(c)+f(d)的最小值.
分析:(1)把f(1)=e+1,f(2)=
-ln2+1代入函数解析式得到关于a,b的方程组,求解方程组可得a,b的值;
(2)把(1)中求得的a,b的值代入函数解析式,由函数单调性求绝对值内部的代数式的范围,从而可求函数f(x)在[1,e2]上的取值范围;
(3)根据c≥d,cd=1,得到c≥1,d=
,把f(c)+f(d)的表达式用含有c的代数式表示,然后根据c的不同取值范围,利用基本不等式求f(c)+f(d)的最小值,最后得出要求的结论.
| e |
| 2 |
(2)把(1)中求得的a,b的值代入函数解析式,由函数单调性求绝对值内部的代数式的范围,从而可求函数f(x)在[1,e2]上的取值范围;
(3)根据c≥d,cd=1,得到c≥1,d=
| 1 |
| c |
解答:解:(1)由f(1)=e+1,f(2)=
-ln2+1.
得:
,
因为a>2,所以,
,解得:a=e,b=1.
(2)由(1)知,f(x)=|lnx-
|+1,
令g(x)=lnx-
,则g′(x)=
+
=
,
当x∈[1,e2]时g′(x)>0恒成立,
所以,g(x)在[1,e2]上为增函数,
所以g(x)min=g(1)=-e,g(x)max=g(e2)=lne2-
=2-
.
所以,|lnx-
|∈[0,e],
则函数f(x)在[1,e2]上的取值范围是[1,e+1].
(3)由c≥d,cd=1,得e≥1,
所以lnc≥0,ce≥0,
若1≤c<e,
f(c)+f(d)=|lnc-
|+|-lnc-ce|+2
=
-lnc+lnc+ce+2=
+ce+2≥2
+2=2e+2.
若c=e,
f(c)+f(d)=|lnc-
|+|-lnc-ce|+2
=e2+3.
若c>e,
f(c)+f(d)=|lnc-
|+|-lnc-ce|+2
=lnc-
+lnc+ce+2
=2lnc+e(c-
)+2,
函数h(c)=2lnc+e(c-
)+2为(e,+∞)上的增函数,
所以,f(c)+f(d)>h(e)=2lne+e(e-
)+2=e2+3.
因为e2+3≥2e+2,
所以,当c=d=1时,f(c)+f(d)的最小值为2e+2.
| e |
| 2 |
得:
|
因为a>2,所以,
|
(2)由(1)知,f(x)=|lnx-
| e |
| x |
令g(x)=lnx-
| e |
| x |
| 1 |
| x |
| e |
| x2 |
| x+e |
| x2 |
当x∈[1,e2]时g′(x)>0恒成立,
所以,g(x)在[1,e2]上为增函数,
所以g(x)min=g(1)=-e,g(x)max=g(e2)=lne2-
| e |
| e2 |
| 1 |
| e |
所以,|lnx-
| e |
| x |
则函数f(x)在[1,e2]上的取值范围是[1,e+1].
(3)由c≥d,cd=1,得e≥1,
所以lnc≥0,ce≥0,
若1≤c<e,
f(c)+f(d)=|lnc-
| e |
| c |
=
| e |
| c |
| e |
| c |
|
若c=e,
f(c)+f(d)=|lnc-
| e |
| c |
=e2+3.
若c>e,
f(c)+f(d)=|lnc-
| e |
| c |
=lnc-
| e |
| c |
=2lnc+e(c-
| 1 |
| c |
函数h(c)=2lnc+e(c-
| 1 |
| c |
所以,f(c)+f(d)>h(e)=2lne+e(e-
| 1 |
| e |
因为e2+3≥2e+2,
所以,当c=d=1时,f(c)+f(d)的最小值为2e+2.
点评:本题考查了利用代入法求函数解析式,考查了利用函数的导函数求闭区间上的最值,考查了分类讨论的数学思想,训练了利用基本不等式求函数的最值,此题属中档题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
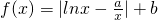 ,若
,若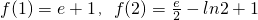 .
.