题目内容

在△ABC中，AB=3，BC=
13
，AC=4，则边AC上的高为______．
∵在△ABC中，AB=3，BC=
13
，AC=4，
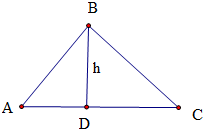
精英家教网

∴由余弦定理，得cosA=
AB2+AC2-BC2
2AB•AC
=
1
2

∴sinA=
1-cos2A
=
3
2

因此，边AC上的高h=ABsinA=3×
3
2
=
3
3
2

故答案为：
3
3
2
练习册系列答案
相关题目
在△ABC中，AB=AC，D、E分别是AB、AC的中点，则（　　）
在△ABC中，AB=4，AC=2，S△ABC=2
3
．
（1）求△ABC外接圆的面积．
（ 2）求cos（2B+
π
3
）的值．
在△ABC中，AB=a，AC=b，当
a
•
b
＜0时，△ABC为
钝角三角形
钝角三角形
．
在△ABC中，AB=2，BC=3，AC=
7
，则△ABC的面积为
3
3
2
3
3
2
，△ABC的外接圆的面积为
7π
3
7π
3
．
在△ABC中，
AB
=
a
，
AC
=
b
，M为AB的中点，
BN
=
1
3
BC
，则
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网