题目内容
已知定义在实数集上的函数fn(x)=xn,n∈N*,其导函数记为fn′(x),且满足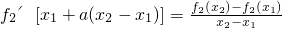 ,a,x1,x2为常数,x1≠x2.
,a,x1,x2为常数,x1≠x2.
(1)试求a的值;
(2)记函数F(x)=b•f1(x)-lnf3(x),x∈(0,e],若F(x)的最小值为6,求实数b的值;
(3)对于(2)中的b,设函数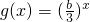 ,A(x1,y1),B(x2,y2)(x1<x2)是函数g(x)图象上两点,若
,A(x1,y1),B(x2,y2)(x1<x2)是函数g(x)图象上两点,若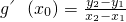 ,试判断x0,x1,x2的大小,并加以证明.
,试判断x0,x1,x2的大小,并加以证明.
解:(1)f2(x)=x2,f2′(x)=2x
依题意,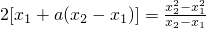 ,得,
,得, .
.
(2)F(x)=bx-3lnx,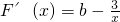 ,x∈(0,e],
,x∈(0,e],
①若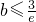 ,
, ,F(x)在(0,e]上单调递减,
,F(x)在(0,e]上单调递减,
F(x)的最小值是F(e),由a1(x),a2(x),a3(x)得,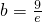 (舍去);
(舍去);
②若 ,
,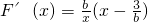 ,令F'(x)=0得
,令F'(x)=0得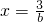 ,
,
当 时,F'(x)<0,F(x)在
时,F'(x)<0,F(x)在 上单调递减;
上单调递减;
当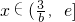 时,F'(x)>0,F(x)在
时,F'(x)>0,F(x)在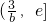 上单调递增;
上单调递增;
所以F(x)的最小值是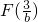 ,由
,由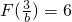 得,b=3e.
得,b=3e.
(3)g(x)=ex,猜测x1<x0<x2.
只需证 ,∵
,∵ ,
,
故只需证 ,
,
即证: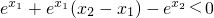 ,且
,且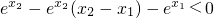 ,
,
设 ,h'(x)=-ex(x-x2),当x≤x2时,h'(x)≥0,
,h'(x)=-ex(x-x2),当x≤x2时,h'(x)≥0,
∴h(x)在(-∞,x2]上是增函数,
∵x1<x2,∴h(x1)<h(x2),即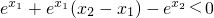 ,
,
设 ,则φ'(x)=-ex(x-x1),当x≥x1时,φ'(x)≤0,
,则φ'(x)=-ex(x-x1),当x≥x1时,φ'(x)≤0,
∴φ(x)在[x1,+∞)上是减函数,
∵x1<x2,∴φ(x1)>φ(x2),即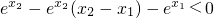 .
.
综上所述,x1<x0<x2.
分析:(1)根据所给的函数,对函数求导,根据题意写出满足的关系式,求出字母系数的值.
(2)根据所给的函数,对函数求导,根据函数求最值的过程,先求出函数的单调性,根据单调性做出函数的单调区间,进一步做出函数的最值.
(3)先猜测三个变量的大小,要证三个变量之间的这种大小关系,只要构造新不等式,只需证 ,结合条件中所给的关系,利用函数的单调性得到结论.
,结合条件中所给的关系,利用函数的单调性得到结论.
点评:本题考查函数的单调区间和单调性的应用,本题解题的关键是猜测和证明的过程非常重要,再者题目要证明一个不等式成立,题目做了铺垫,始终根据函数的性质解题.
依题意,
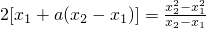 ,得,
,得, .
. (2)F(x)=bx-3lnx,
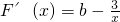 ,x∈(0,e],
,x∈(0,e],①若
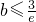 ,
, ,F(x)在(0,e]上单调递减,
,F(x)在(0,e]上单调递减,F(x)的最小值是F(e),由a1(x),a2(x),a3(x)得,
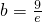 (舍去);
(舍去); ②若
 ,
,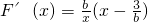 ,令F'(x)=0得
,令F'(x)=0得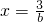 ,
,当
 时,F'(x)<0,F(x)在
时,F'(x)<0,F(x)在 上单调递减;
上单调递减;当
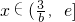 时,F'(x)>0,F(x)在
时,F'(x)>0,F(x)在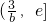 上单调递增;
上单调递增;所以F(x)的最小值是
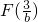 ,由
,由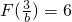 得,b=3e.
得,b=3e. (3)g(x)=ex,猜测x1<x0<x2.
只需证
 ,∵
,∵ ,
,故只需证
 ,
,即证:
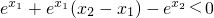 ,且
,且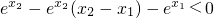 ,
,设
 ,h'(x)=-ex(x-x2),当x≤x2时,h'(x)≥0,
,h'(x)=-ex(x-x2),当x≤x2时,h'(x)≥0,∴h(x)在(-∞,x2]上是增函数,
∵x1<x2,∴h(x1)<h(x2),即
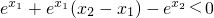 ,
,设
 ,则φ'(x)=-ex(x-x1),当x≥x1时,φ'(x)≤0,
,则φ'(x)=-ex(x-x1),当x≥x1时,φ'(x)≤0,∴φ(x)在[x1,+∞)上是减函数,
∵x1<x2,∴φ(x1)>φ(x2),即
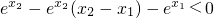 .
.综上所述,x1<x0<x2.
分析:(1)根据所给的函数,对函数求导,根据题意写出满足的关系式,求出字母系数的值.
(2)根据所给的函数,对函数求导,根据函数求最值的过程,先求出函数的单调性,根据单调性做出函数的单调区间,进一步做出函数的最值.
(3)先猜测三个变量的大小,要证三个变量之间的这种大小关系,只要构造新不等式,只需证
 ,结合条件中所给的关系,利用函数的单调性得到结论.
,结合条件中所给的关系,利用函数的单调性得到结论.点评:本题考查函数的单调区间和单调性的应用,本题解题的关键是猜测和证明的过程非常重要,再者题目要证明一个不等式成立,题目做了铺垫,始终根据函数的性质解题.

练习册系列答案
相关题目