题目内容
设向量
=（
，sinα），
=（cosα，
），且
∥
，则锐角α为（ ）
| a |
| 3 |
| 2 |
| b |
| 1 |
| 3 |
| a |
| b |
| A、30° | B、45° |
| C、60° | D、75° |
分析：根据两个向量平行，交叉相乘差为0，我们根据向量
=(
，sinα)，
=(cosα，
)，且
∥
，易得到一个三角方程，根据α为锐角，我们易求出满足条件的值．
| a |
| 3 |
| 2 |
| b |
| 1 |
| 3 |
| a |
| b |
解答：解：∵向量
=(
，sinα)，
=(cosα，
)，
又∵
∥
，
∴cosαsinα-
=0，
即sin2α=1，
又∵α为锐角，
∴α=45°
故选：B
| a |
| 3 |
| 2 |
| b |
| 1 |
| 3 |
又∵
| a |
| b |
∴cosαsinα-
| 1 |
| 2 |
即sin2α=1，
又∵α为锐角，
∴α=45°
故选：B
点评：本题考查的知识点是平面向量共线（平行）的坐标表示，及三角函数的化简求值，其中根据两个向量平行，交叉相乘差为0，构造三角方程是解答本题的关键．
练习册系列答案
相关题目
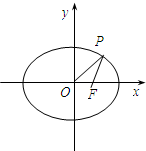如图，F为椭圆