题目内容
(本小题满分12分)如图,PA⊥平面ABCD,ABCD是矩形,PA=AB=1,PD与平面ABCD所成角是30°,点F是PB的中点,点E在边BC上移动.
(Ⅰ)点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(Ⅱ)证明:无论点E在边BC的何处,都有PE⊥AF;
(Ⅲ)当BE等于何值时,二面角P-DE-A的大小为45°.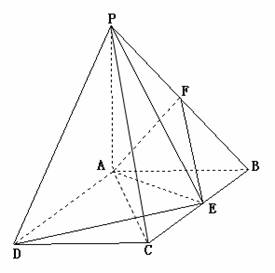
思路点拨:本题是一个开放型问题,考查了线面平行、线面垂直、二面角等知识,考查了同学们解决空间问题的能力。
(Ⅰ)利用三角形的中位线及线面平行的判定定理解决;
(Ⅱ)通过证明![]() 即可解决;
即可解决;
(Ⅲ)作出二面角的平面角,设出BE的长度,然后在直角三角形DCE 中列方程求解BE的长度。本题也可利用向量法解决。
解: 解法一:(Ⅰ)当点![]() 为
为![]() 的中点时,
的中点时,![]() 与平面
与平面![]() 平行.-------1分
平行.-------1分
∵在![]() 中,
中,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,∴
的中点,∴![]() ∥
∥![]() 又
又![]() 平面
平面![]() ,
,
而![]() 平面
平面![]() ∴
∴![]() ∥平面
∥平面![]() . ………4分
. ………4分
(Ⅱ)证明:![]() ,
,
![]() ,又
,又![]()
![]() ,
,
又![]() ,∴
,∴![]() . ---------------------------------6分
. ---------------------------------6分
又![]() ,点
,点![]() 是
是![]() 的中点,
的中点,![]()
![]() ,
,![]() .
.
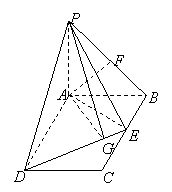
![]() .………8分
.………8分
(Ⅲ)过![]() 作
作![]() 于
于![]() ,连
,连![]() ,
,
又∵![]() ,则
,则![]() 平面
平面![]() ,
,
则![]() 是二面角
是二面角![]() 的平面角,
的平面角,
∴![]() ,………10分
,………10分
∵![]() 与平面
与平面![]() 所成角是
所成角是![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() .
.
∴![]() ,
,![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
 得
得![]() . ………12分
. ………12分
解法二:(向量法)(Ⅰ)同解法一………………4分
(Ⅱ)建立如图所示空间直角坐标系,则![]() ,
,
![]() ,
,![]() ,
,![]() .
.
设![]() ,则
,则![]()
![]() ∴
∴![]() ………8分
………8分
(Ⅲ)设平面![]() 的法向量为
的法向量为![]() ,由
,由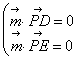 ,得:
,得:![]() ,
,
而平面![]() 的法向量为
的法向量为![]() ,
,
∵二面角![]() 的大小是
的大小是![]() ,所以
,所以![]() =
=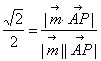 ,
,
∴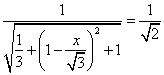 ,
,
得![]() 或
或 ![]() (舍). ………………12分
(舍). ………………12分
归纳总结:无论是线面平行(垂直)还是面面平行(垂直),都源自于线与线的平行(垂直),这种“高维”向“低维”转化的思想方法,在解题时非常重要,在处理实际问题的过程中,可以先从题设条件入手,分析已有的平行(垂直)关系,再从结论入手分析所要证明的平行(垂直)关系,从而架起已知与未知之间的桥梁。 而空间向量是解答立体几何问题的有利工具,它有着快捷有效的特征,是近几年高考中一直考查的重点内容。

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案