题目内容
已知 ,
,(1)若
 ∥
∥ ,求x与y之间的关系式;
,求x与y之间的关系式;(2)在(1)的前提下,若
 ,求向量
,求向量 的模的大小.
的模的大小.
【答案】分析:(1)由向量的坐标运算可得 的坐标,又由
的坐标,又由 ∥
∥ ,可得x(2-y)-y(-x-4)=0,变形可得答案;
,可得x(2-y)-y(-x-4)=0,变形可得答案;
(2)先求出 、
、 的坐标,又由
的坐标,又由 ,可得(x+6)(x-2)+(y+1)(y-3)=0①,结合(1)的结论x+2y=0②,联立①②,解可得x、y的值,可得
,可得(x+6)(x-2)+(y+1)(y-3)=0①,结合(1)的结论x+2y=0②,联立①②,解可得x、y的值,可得 的坐标,进而计算可得|
的坐标,进而计算可得| |,即可得答案.
|,即可得答案.
解答:解:(1) =
= +
+ +
+ =(x+4,y-2),
=(x+4,y-2),
又由 ∥
∥ ,则x(2-y)-y(-x-4)=0,
,则x(2-y)-y(-x-4)=0,
化简可得x+2y=0;
(2) =(x+6,y+1),
=(x+6,y+1), =(x-2,y-3),
=(x-2,y-3),
若 ,
, •
• =0,(x+6)(x-2)+(y+1)(y-3)=0,①
=0,(x+6)(x-2)+(y+1)(y-3)=0,①
又由x+2y=0,②
联立①②可得,y2-2y-3=0,
解可得y=3或y=-1,则x=-6或2,
即 =(-6,3)或(2,-1);
=(-6,3)或(2,-1);
则| |=3
|=3 或
或 .
.
点评:本题考查平面向量数量积的运算,要牢记通过向量的数量积来计算模、夹角以及判断向量平行、垂直的方法.
 的坐标,又由
的坐标,又由 ∥
∥ ,可得x(2-y)-y(-x-4)=0,变形可得答案;
,可得x(2-y)-y(-x-4)=0,变形可得答案;(2)先求出
 、
、 的坐标,又由
的坐标,又由 ,可得(x+6)(x-2)+(y+1)(y-3)=0①,结合(1)的结论x+2y=0②,联立①②,解可得x、y的值,可得
,可得(x+6)(x-2)+(y+1)(y-3)=0①,结合(1)的结论x+2y=0②,联立①②,解可得x、y的值,可得 的坐标,进而计算可得|
的坐标,进而计算可得| |,即可得答案.
|,即可得答案.解答:解:(1)
 =
= +
+ +
+ =(x+4,y-2),
=(x+4,y-2),又由
 ∥
∥ ,则x(2-y)-y(-x-4)=0,
,则x(2-y)-y(-x-4)=0,化简可得x+2y=0;
(2)
 =(x+6,y+1),
=(x+6,y+1), =(x-2,y-3),
=(x-2,y-3),若
 ,
, •
• =0,(x+6)(x-2)+(y+1)(y-3)=0,①
=0,(x+6)(x-2)+(y+1)(y-3)=0,①又由x+2y=0,②
联立①②可得,y2-2y-3=0,
解可得y=3或y=-1,则x=-6或2,
即
 =(-6,3)或(2,-1);
=(-6,3)或(2,-1);则|
 |=3
|=3 或
或 .
.点评:本题考查平面向量数量积的运算,要牢记通过向量的数量积来计算模、夹角以及判断向量平行、垂直的方法.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目

 平行,求
平行,求 的值。
的值。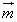 =(1,λsinA),
=(1,λsinA), =(sinA,1+cosA).已知
=(sinA,1+cosA).已知 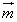 ∥
∥ .
.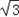 a,求λ的取值范围.
a,求λ的取值范围.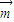 =(1,λsinA),
=(1,λsinA),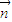 =(sinA,1+cosA).已知
=(sinA,1+cosA).已知 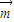 ∥
∥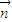 .
.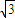 a,求λ的取值范围.
a,求λ的取值范围.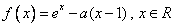 .
.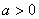 ,求函数
,求函数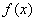 在
在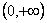 上的极值;
上的极值;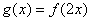 ,设函数
,设函数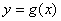 的图象C与
的图象C与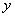 轴交于
轴交于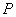 点,曲线C在
点,曲线C在 ,求当
,求当 时
时