题目内容
直线y=kx+1与双曲线x2-y2=1的左支交于A,B两点,另一条直线l过点(-2,0)和AB的中点,则直线l在y轴上的截距b的取值范围为
(-∞,-2-
)∪(2,+∞)
| 2 |
(-∞,-2-
)∪(2,+∞)
.| 2 |
分析:直线与双曲线方程联立消去y,设A(x1,y1)、B(x2,y2),进而根据判别大于0及x1和x2的范围求得k的范围,表示出AB中点的坐标,进而表示出直线l的方程,令x=0求得b关于k的表达式,根据k的范围求得b的范围.
解答:解:由
,得(1-k2)x2-2kx-2=0,
设A(x1,y1)、B(x2,y2),
则
,解得1<k<
,
∴AB中点为(
,
),
∴l方程为y=
,令x=0,
得b=
=
,
∵1<k<
,
∴
-2<-2(k-
)2+
<1,
所以,b的范围是(-∞,-2-
)∪(2,+∞).
故答案为:(-∞,-2-
)∪(2,+∞).
|
设A(x1,y1)、B(x2,y2),
则
|
| 2 |
∴AB中点为(
| k |
| 1-k2 |
| 1 |
| 1-k2 |
∴l方程为y=
| x+2 |
| -2k2+k+2 |
得b=
| 2 |
| -2k2+k+2 |
| 2 | ||||
-2(k-
|
∵1<k<
| 2 |
∴
| 2 |
| 1 |
| 4 |
| 17 |
| 8 |
所以,b的范围是(-∞,-2-
| 2 |
故答案为:(-∞,-2-
| 2 |
点评:本题主要考查了直线与圆锥曲线综合问题.用k表示b的过程即是建立目标函数的过程,本题要注意k的取值范围.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
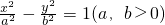 的虚轴长为2
的虚轴长为2 ,渐近线方程是y=
,渐近线方程是y=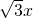 ,O为坐标原点,直线y=kx+m(k,m∈R)与双曲线C相交于A、B两点,且
,O为坐标原点,直线y=kx+m(k,m∈R)与双曲线C相交于A、B两点,且 .
. 的虚轴长为2
的虚轴长为2 ,渐近线方程是y=
,渐近线方程是y= ,O为坐标原点,直线y=kx+m(k,m∈R)与双曲线C相交于A、B两点,且
,O为坐标原点,直线y=kx+m(k,m∈R)与双曲线C相交于A、B两点,且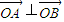 .
.