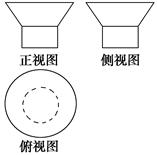
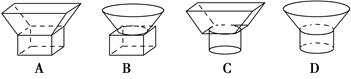
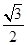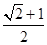题目内容
用一个平行于棱锥底面的平面截这个棱锥,截得的棱台上、下底面面积比为 ,截去的棱锥的高是
,截去的棱锥的高是 ,则棱台的高是( )
,则棱台的高是( )
A. | B. | C. | D. |
D
解析试题分析:如下图,设截面圆 的半径为
的半径为 ,底面圆的半径为
,底面圆的半径为 ,则依题意有
,则依题意有 且
且 ,由三角形
,由三角形 与
与 相似可得
相似可得 ,所以
,所以 ,所以
,所以 ,故选D.
,故选D.
考点:圆锥的结构特征与性质.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
已知某几何体的三视图如图所示,其中俯视图中圆的直径为4,该几何体的体积为V1,直径为4的球的体积为V2,则V1:V2等于( )
| A.1:2 |
| B.2:1 |
| C.1:1 |
| D.1:4 |
己知某几何体的三视图如图所示,则该几何体的体积是( )
A. | B. | C. | D.2 |
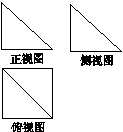
三棱柱的直观图和三视图(正视图和俯视图是正方形,侧视图是等腰直角三角形)如图所示,则这个三棱柱的表面积等于( )

A.12+4 | B.6+2 |
C.8+4 | D.4 |
一几何体的三视图如图所示,则该几何体的体积为( )、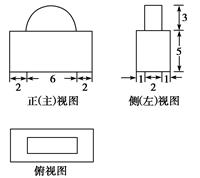
| A.200+9π | B.200+18π |
| C.140+9π | D.140+18π |
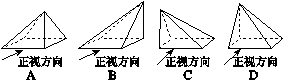
一个几何体的三视图如图所示,该几何体从上到下由四个简单几何体组成,其体积分别记为V1,V2,V3,V4,上面两个简单几何体均为旋转体,下面两个简单几何体均为多面体,则有( )
| A.V1<V2<V4<V3 | B.V1<V3<V2<V4 |
| C.V2<V1<V3<V4 | D.V2<V3<V1<V4 |
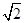 的矩形,则该正方体的正视图的面积等于( )
的矩形,则该正方体的正视图的面积等于( )