题目内容
如图所示，在正方体ABCD-A1B1C1D1中，M，N分别是对角线AB1，BC1上的点，且| B1M |
| MA |
| C1N |
| NB |
分析：在平面AA1B1B内，作MK∥AB，交BB1于K点，连接KN，利用“面面平行”⇒“线面平行”即可．
解答：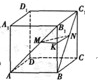
证明：在平面AA1B1B内，作MK∥AB，交BB1于K点，连接KN，
则易知
=
；
∵
=
，
∴
=
，
∴KN∥B1C1，又A1B1∥AB，
∴MK∥A1B1．
∴平面MKN∥平面A1B1C1D1，而MN?平面MKN，
∴MN∥平面A1B1C1D1．
证明：在平面AA1B1B内，作MK∥AB，交BB1于K点，连接KN，则易知
| B1M |
| MA |
| B1K |
| KB |
∵
| B1M |
| MA |
| C1N |
| NB |
∴
| B1K |
| KB |
| C1N |
| NB |
∴KN∥B1C1，又A1B1∥AB，
∴MK∥A1B1．
∴平面MKN∥平面A1B1C1D1，而MN?平面MKN，
∴MN∥平面A1B1C1D1．
点评：本题考查直线与平面平行的判定，考查作辅助线进行推理证明的能力，属于中档题．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
相关题目
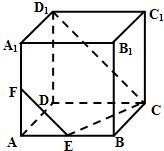如图所示，在正方体ABCD-A1B1C1D1中，E为AB的中点
（2011•宝山区二模）如图所示，在正方体ABCD-A1B1C1D1的侧面ABB1A1内有一动点P到直线A1B1和直线BC的距离相等，则动点P所在曲线形状为（ ）
如图所示，在正方体ABCD-A1B1C1D1的侧面AB1内有一动点P到直线A1B1与直线BC的距离相等，则动点P所在曲线的形状为（ ）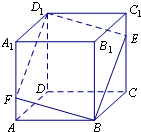
如图所示，在正方体ABCD-A1B1C1D1中，点E是棱CC1上的一个动点，平面BED1交棱AA1于点F．则下列命题中假命题是（ ）