Question

【题目】在直角坐标系xOy中，曲线C1的参数方程为 （α为参数，﹣π＜α＜0），曲线C2的参数方程为 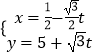（t为参数），以O为极点，x轴的正半轴为极轴建立极坐标系．
（1）求曲线C1的极坐标方程和曲线C2的普通方程；
（2）射线θ=﹣ 与曲线C1的交点为P，与曲线C2的交点为Q，求线段PQ的长．

Answer 1

【答案】
（1）解：曲线C1的参数方程为 （α为参数，﹣π＜α＜0），

普通方程为（x﹣1）2+y2=1，（y＜0），

极坐标方程为ρ=2cosθ，θ∈（﹣ ，0），曲线C2的参数方程为 （t为参数），

普通方程2x+y﹣6=0；

（2）θ=﹣ ， ，即P（ ，﹣ ）；

θ=﹣ 代入曲线C2的极坐标方程，可得ρ′=6 ，即Q（6 ，﹣ ），

∴|PQ|=6 ﹣ =5 ．

【解析】（1）根据同角三角函数关系进行消参可得到C1的普通方程，再转化为极坐标方程，将C2的参数方程消掉t可得到普通方程，（2）将θ=-，代入两个曲线的极坐标方程，得到P、Q的坐标，从而得到线段PQ的长.