题目内容
13.已知数列{an}满足an+1=an -an-1 (n≥2),a1=1,a2=3,记Sn=a1+a2+…+an ,则S102=0.分析 求出数列的前几项,确定数列{an}是以6为周期的周期数列,求出通过周期各项和,即可得到结论.
解答 解:∵数列{an}满足an+1=an-an-1(n≥2),a1=1,a2=3,
∴a3=2,a4=-1,a5=-3,a6=-2,a7=1,…,
∴数列{an}是以6为周期的周期数列,
∵102=6×17,并且a1+a2+a3+a4+a5+a6=0,
∴S102=0
故答案为:0.
点评 本题考查数列递推式,考查正确数列,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
4.cos$\frac{28π}{3}$=( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{{\sqrt{3}}}{2}$ |
8.设函数y=f(x)(x∈R)的导函数为f′(x),且f(x)=f(-x),f′(x)<f(x),则下列不等式成立的是( )
| A. | f(0)<e-1f(1)<e2f(2) | B. | e-1f(1)<f(0)<e2f(2) | C. | e2f(2)<e-1f(1)<f(0) | D. | e2f(2)<f(0)<e-1f(1) |
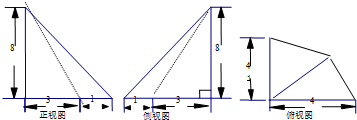 已知某空间几何体的三视图如图所示,则该几何体的体积是32.
已知某空间几何体的三视图如图所示,则该几何体的体积是32.