题目内容
已知不等式 的解集为
的解集为 .
.
(1)求 ,
, 的值;
的值;
(2)求函数
 的最小值.
的最小值.
 的解集为
的解集为 .
.(1)求
 ,
, 的值;
的值;(2)求函数

 的最小值.
的最小值.(1)  ,
, ;(2) 12.
;(2) 12.
 ,
, ;(2) 12.
;(2) 12.;
试题分析:(1)根据一元次不等式与一元二次函数的关系可知:1和 是方程
是方程 的两根;
的两根;
利用一元二次方程根与系数的关系建立方程组,可解得 ,
, 的值;
的值;
(2)由(1)的结果可确定 的解析式及定义域,根据解析表达式的特点及定义域的情况,可选择采用导数法或基本不等式法求函数
的解析式及定义域,根据解析表达式的特点及定义域的情况,可选择采用导数法或基本不等式法求函数 的最小值.
的最小值.
试题解析:(1)∵不等式 的解集为
的解集为
∴1和 是方程
是方程 的两根 2分
的两根 2分
∴
解得 ,
, 7分
7分
(2)由(1)得 9分
9分
 11分
11分
=12 12分
当且仅当 ,即
,即 时,函数
时,函数 有最小值12 14分
有最小值12 14分
试题分析:(1)根据一元次不等式与一元二次函数的关系可知:1和
 是方程
是方程 的两根;
的两根;利用一元二次方程根与系数的关系建立方程组,可解得
 ,
, 的值;
的值;(2)由(1)的结果可确定
 的解析式及定义域,根据解析表达式的特点及定义域的情况,可选择采用导数法或基本不等式法求函数
的解析式及定义域,根据解析表达式的特点及定义域的情况,可选择采用导数法或基本不等式法求函数 的最小值.
的最小值.试题解析:(1)∵不等式
 的解集为
的解集为
∴1和
 是方程
是方程 的两根 2分
的两根 2分∴

解得
 ,
, 7分
7分(2)由(1)得
 9分
9分 11分
11分=12 12分
当且仅当
 ,即
,即 时,函数
时,函数 有最小值12 14分
有最小值12 14分
练习册系列答案
相关题目
 的解集与关于
的解集与关于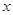 的不等式
的不等式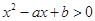 的解集相同.
的解集相同.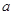 ,
,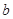 的值;
的值;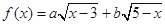 的最大值,以及取得最大值时
的最大值,以及取得最大值时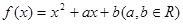 ,方程
,方程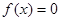 有两个相等的实数根,若关于
有两个相等的实数根,若关于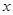 的不等式
的不等式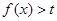 的解集为
的解集为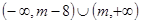 ,则实数
,则实数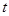 的值为 .
的值为 . :实数
:实数 满足
满足 ,其中
,其中 ;命题
;命题 :实数
:实数 且
且 的必要不充分条件,则实数
的必要不充分条件,则实数 的取值范围是 .
的取值范围是 . 的解集为
的解集为 ,则
,则 的解集为 ( )
的解集为 ( )



 的解集为( )
的解集为( )




 的解集是
的解集是 ,则
,则 的值是( )。
的值是( )。


