题目内容
已知椭圆C1: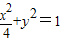 ,双曲线C2:
,双曲线C2: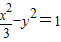 .若直线
.若直线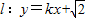 与椭圆C1、双曲线C2都恒有两个不同的交点,且l与C2的两交点A、B满足
与椭圆C1、双曲线C2都恒有两个不同的交点,且l与C2的两交点A、B满足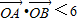 (其中O为原点),求k的取值范围.
(其中O为原点),求k的取值范围.
【答案】分析:由l与椭圆C1恒有两个不同的交点,可得解得  ①,由l与C2 有两个不同的交点可得 k2≠
①,由l与C2 有两个不同的交点可得 k2≠ ,且k2<1 ②,再由
,且k2<1 ②,再由 可得
可得 或
或 ③,结合①②③求得k2的取值范围,即可得到k的取值范围.
③,结合①②③求得k2的取值范围,即可得到k的取值范围.
解答:解:将 代入
代入 得,
得, ,
,
由判别式 ,解得
,解得  ①.
①.
将 代入
代入 得,(1-3k2)x2-6
得,(1-3k2)x2-6 kx-9=0,
kx-9=0,
由l与C2 有两个不同的交点可得 ,解得 k2≠
,解得 k2≠ ,且k2<1 ②,
,且k2<1 ②,
根据 =x1x2+y1y2=(k2+1)x1x2+
=x1x2+y1y2=(k2+1)x1x2+ +2=
+2= <6,
<6,
解得 ,或
,或 ③. 由①②③得
③. 由①②③得 ,或
,或 .
.
故k的取值范围为: .
.
点评:本题考查直线和圆锥曲线的位置关系的应用,两个向量的数量积公式的应用,求得 ,或
,或 ,是解题的难点和关键.
,是解题的难点和关键.
 ①,由l与C2 有两个不同的交点可得 k2≠
①,由l与C2 有两个不同的交点可得 k2≠ ,且k2<1 ②,再由
,且k2<1 ②,再由 可得
可得 或
或 ③,结合①②③求得k2的取值范围,即可得到k的取值范围.
③,结合①②③求得k2的取值范围,即可得到k的取值范围.解答:解:将
 代入
代入 得,
得, ,
,由判别式
 ,解得
,解得  ①.
①.将
 代入
代入 得,(1-3k2)x2-6
得,(1-3k2)x2-6 kx-9=0,
kx-9=0,由l与C2 有两个不同的交点可得
 ,解得 k2≠
,解得 k2≠ ,且k2<1 ②,
,且k2<1 ②,根据
 =x1x2+y1y2=(k2+1)x1x2+
=x1x2+y1y2=(k2+1)x1x2+ +2=
+2= <6,
<6,解得
 ,或
,或 ③. 由①②③得
③. 由①②③得 ,或
,或 .
.故k的取值范围为:
 .
.点评:本题考查直线和圆锥曲线的位置关系的应用,两个向量的数量积公式的应用,求得
 ,或
,或 ,是解题的难点和关键.
,是解题的难点和关键. 
练习册系列答案
相关题目
 与双曲线C2:
与双曲线C2: 有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A、B两点,C1恰好将线段AB三等分,则( )
有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A、B两点,C1恰好将线段AB三等分,则( ) B.
B. C.
C. D.
D.
 与双曲线C2:
与双曲线C2: 有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A、B两点.若C1恰好将线段
有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A、B两点.若C1恰好将线段 三等分,则( )
三等分,则( ) B.
B. C.
C. D.
D.
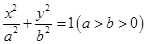 与双曲线C2:
与双曲线C2: 有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A、B两点.若C1恰好将线段
有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A、B两点.若C1恰好将线段 三等分,则( )
三等分,则( ) B.
B. C.
C. D.
D.
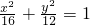 ,双曲线C2与C1具有相同的焦点,且离心率互为倒数.
,双曲线C2与C1具有相同的焦点,且离心率互为倒数.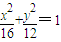 ,双曲线C2与C1具有相同的焦点,且离心率互为倒数.
,双曲线C2与C1具有相同的焦点,且离心率互为倒数.