题目内容
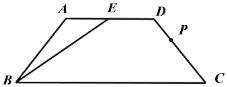
【题目】如图，在等腰梯形
中，
，
，高为
，
为
的中点，
为折线段
上的动点，设
的最小值为
，若关于的方程
有两不等实根，则实数
的取值范围是（ ）
A.
B.
C.
D.
【答案】A
【解析】
先以
为坐标原点，
为
轴，建立直角坐标系，设
的横坐标为，将
用表示分段表示出来，再求最小值
，再对
有两不等实根变形，可转化为两函数有两个交点，数形结合，求出
的取值范围.
解：以为坐标原点，为轴，建立直角坐标系如图所示:
则
，
，
，
，
设的横坐标为，则
当
时，在
上动，
，则
当
时，的最小值
；
当
，时，在
上动，则
，
则
，
当
时，的最小值
又
，
故，
，
又有两不等实根，则
在有两不等实根，
则
在
有两不等实根，
则
与
，有两个交点.
当
时，有最小值为
，当
时，
，当
时，
，
则，的图象如图所示，
即方程有两不等实根有：
.
故选：A
【题目】有标号分别为1，2，3，4，5，6的6张抗疫宣传海报，要求排成2行3列，则共有_______种不同的排法，如果再要求每列中前面一张的标号比其后面一张的标号小，则共有_______种不同的排法.
【题目】疫情过后，某商场开业一周累计生成2万张购物单，从中随机抽出100张，对每单消费金额进行统计得到下表：
消费金额（单位：元） |
|
|
|
|
|
购物单张数 | 25 | 25 | 30 | ？ | ？ |
由于工作人员失误，后两栏数据已无法辨识，但当时记录表明，根据由以上数据绘制成的频率分布直方图所估计出的每单消费额的中位数与平均数恰好相等（用频率估计概率），完成下列问题：
（1）估计该商场开业一周累计生成的购物单中，单笔消费额超过800元的购物单张数；
（2）为鼓励顾客消费，拉动内需，该商场打算在今年国庆期间进行促销活动，凡单笔消费超过600元者，可抽奖一次，中一等奖、二等奖、三等奖的顾客可以分别获得价值
元、
元、
元的奖品.已知中奖率为100%，且一等奖、二等奖、三等奖的中奖率依次构成等差数列，其中一等奖的中奖率为
.若今年国庆期间该商场的购物单数量预计比疫情后开业一周的购物单数量增长5%，试预测商场今年国庆期间采办奖品的开销.
