题目内容
已知函数f(x)=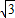 cos2x
cos2x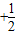 sin2x.
sin2x.(Ⅰ)求f(x)的最小正周期;
(Ⅱ)求f(x)在区间[
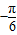 ,
,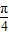 ]上的最大值和最小值.
]上的最大值和最小值.
【答案】分析:(Ⅰ)根据二倍角的余弦、两角和的正弦公式化简解析式,再求出函数的最小正周期;
(Ⅱ)由x的范围求出“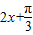 ”的范围,再由正弦函数的最值求出此函数的最值,以及对应的x的值.
”的范围,再由正弦函数的最值求出此函数的最值,以及对应的x的值.
解答:解:(Ⅰ)由题意得,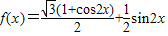
=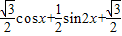
=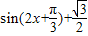
则f(x)的最小正周期T=π
(Ⅱ)∵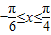 ,∴
,∴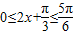 ,
,
当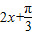 =
=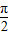 时,即x=
时,即x=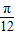 时,f(x)的最大值为1+
时,f(x)的最大值为1+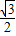 ,
,
当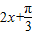 =0时,即x=
=0时,即x=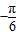 时,f(x)的最小值为
时,f(x)的最小值为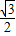 .
.
点评:本题考查了二倍角的余弦、两角和的正弦公式,以及正弦函数的最值的应用,考查了整体思想.
(Ⅱ)由x的范围求出“
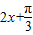 ”的范围,再由正弦函数的最值求出此函数的最值,以及对应的x的值.
”的范围,再由正弦函数的最值求出此函数的最值,以及对应的x的值.解答:解:(Ⅰ)由题意得,
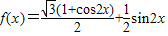
=
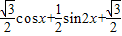
=
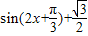
则f(x)的最小正周期T=π
(Ⅱ)∵
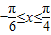 ,∴
,∴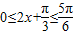 ,
,当
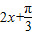 =
=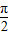 时,即x=
时,即x=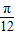 时,f(x)的最大值为1+
时,f(x)的最大值为1+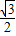 ,
,当
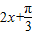 =0时,即x=
=0时,即x=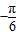 时,f(x)的最小值为
时,f(x)的最小值为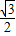 .
.点评:本题考查了二倍角的余弦、两角和的正弦公式,以及正弦函数的最值的应用,考查了整体思想.

练习册系列答案
相关题目
已知函数f(x)=
,则关于x的方程f2(x)+bf(x)+c=0有5个不同实数解的充要条件是( )
|
| A、b<-2且c>0 |
| B、b>-2且c<0 |
| C、b<-2且c=0 |
| D、b≥-2且c=0 |
 已知函数f(x)的图象如图所示,则函数的值域为( )
已知函数f(x)的图象如图所示,则函数的值域为( )