题目内容
已知f（x）是一次函数，且f[f（x）]=x+4，则f（1）=________．
3
分析：由f（x）是一次函数，f[f（x）]=x+4，能够推导出f（x）=x+2，由此能求出f（1）．
解答：∵f（x）是一次函数，
∴设f（x）=kx+b，k≠0，
∴f（f（x））=k（kx+b）+b=k2x+kb+b，
∵f[f（x）]=x+4，
∴
，
解得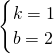
，或
，（舍）
∴f（x）=x+2，
∴f（1）=1+2=3．
故答案为：3．
点评：本题考查函数值的求法，是基础题．解题时要认真审题，仔细解答．
分析：由f（x）是一次函数，f[f（x）]=x+4，能够推导出f（x）=x+2，由此能求出f（1）．
解答：∵f（x）是一次函数，
∴设f（x）=kx+b，k≠0，
∴f（f（x））=k（kx+b）+b=k2x+kb+b，
∵f[f（x）]=x+4，
∴
，解得
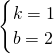，或，（舍）∴f（x）=x+2，
∴f（1）=1+2=3．
故答案为：3．
点评：本题考查函数值的求法，是基础题．解题时要认真审题，仔细解答．
练习册系列答案
华东师大版一课一练系列答案
孟建平名校考卷系列答案
相关题目